如图,四边形 是正方形,曲线 是由一段段90度的弧组成的.其中: 的圆心为点 ,半径为 ; 的圆心为点 ,半径为 ; 的圆心为点 ,半径为 ; 的圆心为点 ,半径为 ; , 的圆心依次按点 , , , 循环.若正方形 的边长为1,则 的长是 .

如图, 的外角 的平分线与它的外接圆相交于点 ,连接 , ,过点 作 ,交 于点 .
求证:(1) ;
(2) 为 的切线.

如图,点 是半圆圆心, 是半圆的直径,点 , 在半圆上,且 , , ,过点 作 于点 ,则阴影部分的面积是 .
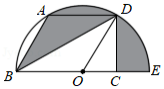
如图, 是 的切线,点 为切点, 交 于点 , ,点 在 上, .则 等于
| A. |
|
B. |
|
C. |
|
D. |
|
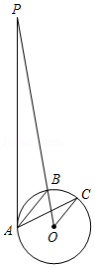
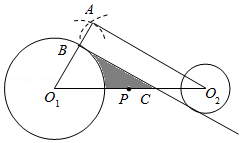
已知 的半径为 , 的半径为 .以 为圆心,以 的长为半径画弧,再以线段 的中点 为圆心,以 的长为半径画弧,两弧交于点 ,连接 , , 交 于点 ,过点 作 的平行线 交 于点 .
(1)求证: 是 的切线;
(2)若 , , ,求阴影部分的面积.
如图,在 中, 为直径, .点 为弦 的中点,点 为 上任意一点.则 的大小可能是
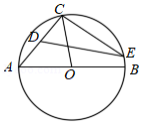
A. B. C. D.
如图,在 中, ,以 的边 为直径作 ,交 于点 ,过点 作 ,垂足为点 .
(1)试证明 是 的切线;
(2)若 的半径为5, ,求此时 的长.

如图,有一块半径为 ,圆心角为 的扇形铁皮,要把它做成一个圆锥形容器(接缝忽略不计),那么这个圆锥形容器的高为

A. B. C. D.
如图, 是 的直径,弦 ,垂足为点 ,连接 , .如果 , ,那么图中阴影部分的面积是

A. B. C. D.
我们把方程 称为圆心为 、半径长为 的圆的标准方程.例如,圆心为 、半径长为3的圆的标准方程是 .在平面直角坐标系中, 与轴交于点 , ,且点 的坐标为 ,与 轴相切于点 ,过点 , , 的抛物线的顶点为 .
(1)求 的标准方程;
(2)试判断直线 与 的位置关系,并说明理由.

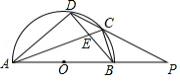
如图,在四边形 中,以 为直径的半圆 经过点 , . 与 相交于点 , ,分别延长 , 相交于点 , , .则 的长是 .