初中数学圆试题

将一物体（视为边长为 $\frac{2}{\pi }$ 米的正方形 $\mathit{ABCD})$ 从地面 $\mathit{PQ}$ 上挪到货车车厢内．如图所示，刚开始点 $B$ 与斜面 $\mathit{EF}$ 上的点 $E$ 重合，先将该物体绕点 $B$ （E）按逆时针方向旋转至正方形 $A_{1}B{C}_1{D}_1$ 的位置，再将其沿 $\mathit{EF}$ 方向平移至正方形 $A_2{B}_2{C}_2{D}_2$ 的位置（此时点 $B_2$ 与点 $G$ 重合），最后将物体移到车厢平台面 $\mathit{MG}$ 上．已知 $\mathit{MG}//\mathit{PQ}$ ， $\angle \mathit{FBP}=30°$ ，过点 $F$ 作 $\mathit{FH}\perp \mathit{MG}$ 于点 $H$ ， $\mathit{FH}=\frac{1}{3}$ 米， $\mathit{EF}=4$ 米．

（1）求线段 $\mathit{FG}$ 的长度；

（2）求在此过程中点 $A$ 运动至点 $A_2$ 所经过的路程．

如图，在 $\text{Rt}\Delta \text{AOB}$ 中， $\angle \mathit{ABO}=90°$ ， $\angle \mathit{OAB}=30°$ ，以点 $O$ 为圆心， $\mathit{OB}$ 为半径的圆交 $\mathit{BO}$ 的延长线于点 $C$ ，过点 $C$ 作 $\mathit{OA}$ 的平行线，交 $\odot O$ 于点 $D$ ，连接 $\mathit{AD}$ ．

（1）求证： $\mathit{AD}$ 为 $\odot O$ 的切线；

（2）若 $\mathit{OB}=2$ ，求弧 $\mathit{CD}$ 的长．

某同学在数学实践活动中，制作了一个侧面积为 $60\pi$ ，底面半径为6的圆锥模型（如图所示），则此圆锥的母线长为 　　．

某种冰激凌的外包装可以视为圆锥，它的底面圆直径 $\mathit{ED}$ 与母线 $\mathit{AD}$ 长之比为 $1:2$ ．制作这种外包装需要用如图所示的等腰三角形材料，其中 $\mathit{AB}=\mathit{AC}$ ， $\mathit{AD}\perp \mathit{BC}$ ．将扇形 $\mathit{AEF}$ 围成圆锥时， $\mathit{AE}$ ， $\mathit{AF}$ 恰好重合．

（1）求这种加工材料的顶角 $\angle \mathit{BAC}$ 的大小．

（2）若圆锥底面圆的直径 $\mathit{ED}$ 为 $5\mathit{cm}$ ，求加工材料剩余部分（图中阴影部分）的面积．（结果保留 $\pi )$

如图，点 $A$ 在以 $\mathit{BC}$ 为直径的 $\odot O$ 上， $\angle \mathit{ABC}$ 的角平分线与 $\mathit{AC}$ 相交于点 $E$ ，与 $\odot O$ 相交于点 $D$ ，延长 $\mathit{CA}$ 至 $M$ ，连结 $\mathit{BM}$ ，使得 $\mathit{MB}=\mathit{ME}$ ，过点 $A$ 作 $\mathit{BM}$ 的平行线与 $\mathit{CD}$ 的延长线交于点 $N$ ．

（1）求证： $\mathit{BM}$ 与 $\odot O$ 相切；

（2）试给出 $\mathit{AC}$ 、 $\mathit{AD}$ 、 $\mathit{CN}$ 之间的数量关系，并予以证明．

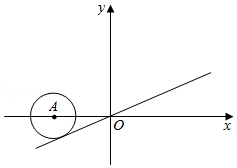
如图，直角坐标系中，以5为半径的动圆的圆心 $A$ 沿 $x$ 轴移动，当 $\odot A$ 与直线 $l:y=\frac{5}{12}x$ 只有一个公共点时，点 $A$ 的坐标为 $($ 　　 $)$

A．

$(-12,0)$

B．

$(-13,0)$

C．

$(\pm 12,0)$

D．

$(\pm 13,0)$

如图，在半径为 $5\mathit{cm}$ 的 $\odot O$ 中， $\mathit{AB}$ 是 $\odot O$ 的直径， $\mathit{CD}$ 是过 $\odot O$ 上一点 $C$ 的直线，且 $\mathit{AD}\perp \mathit{DC}$ 于点 $D$ ， $\mathit{AC}$ 平分 $\angle \mathit{BAD}$ ， $E$ 是 $\mathit{BC}$ 的中点， $\mathit{OE}=3\mathit{cm}$ ．

（1）求证： $\mathit{CD}$ 是 $\odot O$ 的切线；

（2）求 $\mathit{AD}$ 的长．

如图，在 $\odot O$ 中， $\mathit{OA}=3$ ， $\angle C=45°$ ，则图中阴影部分的面积是 　　．（结果保留 $\pi )$

如图， $\mathit{AB}$ 是 $\odot O$ 的直径， $D$ 为 $\odot O$ 上一点， $E$ 为 $\stackrel{̂}{\mathit{BD}}$ 的中点，点 $C$ 在 $\mathit{BA}$ 的延长线上，且 $\angle \mathit{CDA}=\angle B$ ．

（1）求证： $\mathit{CD}$ 是 $\odot O$ 的切线；

（2）若 $\mathit{DE}=2$ ， $\angle \mathit{BDE}=30°$ ，求 $\mathit{CD}$ 的长．

如图，在 $\text{Rt}\Delta \text{ABC}$ 中， $\angle \mathit{ABC}=90°$ ，以 $\mathit{AB}$ 的中点 $O$ 为圆心， $\mathit{AB}$ 为直径的圆交 $\mathit{AC}$ 于 $D$ ， $E$ 是 $\mathit{BC}$ 的中点， $\mathit{DE}$ 交 $\mathit{BA}$ 的延长线于 $F$ ．

（1）求证： $\mathit{FD}$ 是圆 $O$ 的切线：

（2）若 $\mathit{BC}=4$ ， $\mathit{FB}=8$ ，求 $\mathit{AB}$ 的长．

如图， $\mathit{AB}$ 是 $\odot O$ 的直径， $\mathit{BC}$ 是 $\odot O$ 的弦，先将 $\widehat{\mathit{BC}}$ 沿 $\mathit{BC}$ 翻折交 $\mathit{AB}$ 于点 $D$ ，再将 $\widehat{\mathit{BD}}$ 沿 $\mathit{AB}$ 翻折交 $\mathit{BC}$ 于点 $E$ ．若 $\widehat{\mathit{BE}}=\widehat{\mathit{DE}}$ ，设 $\angle \mathit{ABC}=\alpha$ ，则 $\alpha$ 所在的范围是 $($ 　　 $)$

A．	$21.9°<\alpha <22.3°$	B．	$22.3°<\alpha <22.7°$
C．	$22.7°<\alpha <23.1°$	D．	$23.1°<\alpha <23.5°$

如图， $\mathit{\Delta ABC}$ 内接于 $\odot O$ ， $\angle \mathit{BAC}=120°$ ， $\mathit{AB}=\mathit{AC}$ ， $\mathit{BD}$ 是 $\odot O$ 的直径，若 $\mathit{AD}=3$ ，则 $\mathit{BC}=($ 　　 $)$

A．

$2\sqrt{3}$

B．

$3\sqrt{3}$

C．

3

D．

4

筒车是我国古代发明的一种水利灌溉工具，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理，如图1．筒车盛水桶的运行轨道是以轴心 $O$ 为圆心的圆，如图2．已知圆心 $O$ 在水面上方，且 $\odot O$ 被水面截得的弦 $\mathit{AB}$ 长为6米， $\odot O$ 半径长为4米．若点 $C$ 为运行轨道的最低点，则点 $C$ 到弦 $\mathit{AB}$ 所在直线的距离是 $($ 　　 $)$

A．

1米

B．

$(4-\sqrt{7})$ 米

C．

2米

D．

$(4+\sqrt{7})$ 米

如图，等腰 $\mathit{\Delta AOB}$ 中，顶角 $\angle \mathit{AOB}=40°$ ，用尺规按①到④的步骤操作：

①以 $O$ 为圆心， $\mathit{OA}$ 为半径画圆；

②在 $\odot O$ 上任取一点 $P$ （不与点 $A$ ， $B$ 重合），连接 $\mathit{AP}$ ；

③作 $\mathit{AB}$ 的垂直平分线与 $\odot O$ 交于 $M$ ， $N$ ；

④作 $\mathit{AP}$ 的垂直平分线与 $\odot O$ 交于 $E$ ， $F$ ．

结论Ⅰ：顺次连接 $M$ ， $E$ ， $N$ ， $F$ 四点必能得到矩形；

结论Ⅱ： $\odot O$ 上只有唯一的点 $P$ ，使得 $S_{\mathit{扇形}\mathit{FOM}}=S_{\mathit{扇形}\mathit{AOB}}$ ．

对于结论Ⅰ和Ⅱ，下列判断正确的是 $($ 　　 $)$

A．

Ⅰ和Ⅱ都对

B．

Ⅰ和Ⅱ都不对

C．

Ⅰ不对Ⅱ对

D．

Ⅰ对Ⅱ不对

学习圆的性质后，小铭与小熹就讨论起来，小铭说："被直径平分的弦也与直径垂直"，小熹说："用反例就能说明这是假命题"．下列判断正确的是 $($ 　　 $)$

A．	两人说的都对
B．	小铭说的对，小熹说的反例不存在
C．	两人说的都不对
D．	小铭说的不对，小熹说的反例存在