如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形
的边长为7cm,则正方形A,B,C,D的面积之和为_______cm2.
 |
|||
|
|||
按如图所示,把一张边长超过10的正方形纸片剪成5个部分,则中间小正方形(阴影部分)的面积为 
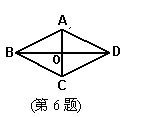
如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.
则以下四个结论中正确结论的个数为( )
①OH= BF; ②∠CHF=45°; ③GH=
BF; ②∠CHF=45°; ③GH= BC;④DH2=HE·HB
BC;④DH2=HE·HB
A. 1个 B. 2个 C. 3个 D. 4个
如图,AB是⊙O的直径,点P是⊙O上的动点(P与A,B不重合),连结AP,PB,过点O分别作OE⊥AP于E,OF⊥BP于F.
若AB=12,当点P在⊙O上运动时,线段EF的长会不会改变.若会改变,请说明理由;若不会改变,请求出EF的长
若AP=BP,求证四边形OEPF是正方形
在图1至图3中,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和CDHN都是正方形.AE的中点是M.
如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,
求证:FM = MH,FM⊥MH将图-1中的CE绕点C顺时针旋转一个锐角,得到图2,
求证:△FMH是等腰直角三角形将图2中的CE缩短到图3的情况,△FMH还是等腰直角三角形吗?(不必
说明理由)
如图,已知菱形ABCD的周长为16,∠ABC=60º,则菱形的面积为 ( )
A.  B.
B. 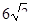 C.
C.  D.
D. 
如图①,在正方形ABCD中,点E、F分别为边BC、CD的 中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE。(不需要证明)
中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE。(不需要证明)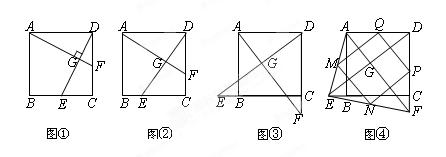
如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF。则上面的结论①、②是否仍然成立?(请直接回答“成立”或“不成立”)
如图③,若点E、F分别在正方形ABCD的边CB的延长线和D
 C的延长线上
C的延长线上 ,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由。
,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由。如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种?
 并写出证明过程。
并写出证明过程。
如图,□ABCD的周长是36,且AB∶BC=5∶4,对角线AC、BD相交于点O,且BD⊥AD,求OB的长。
如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,则DN+MN的最小值为__________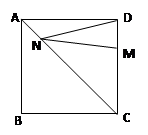
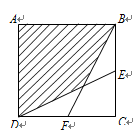
如图,正方形ABCD的边长为4cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是 ____________ cm2.