如图,正方形 中,
中,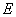 与
与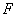 分别是
分别是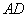 、
、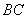 上一点.在
上一点.在
①  、 ②
、 ② 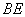 ∥
∥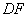 、 ③
、 ③ 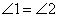 中,
中,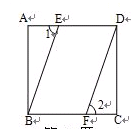
选择其中一个条件,证明
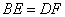
你选择的条件是 (只需填写序号)
如图是一个由正方形ABCD和半圆O组成的封闭图形,点O是圆心.点P从点A出发,沿线段AB、弧BC和线段CD匀速运动,到达终点D.运动过程中OP扫过的面积(s)随时间(t)变化的图象大致是( ) 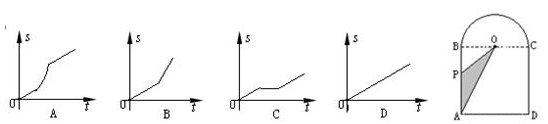
如图,小亮拿一张矩形纸图(1),沿虚线对折一次得图(2),下将对角两顶点重合折叠得图(3)。按图(4)沿折痕中点与重合顶点的连线剪开,得到三个图形,这三个图形分别是( )。(考查动手及空间想象能力等)
| A.都是等腰梯形 | B.两个直角三角形,一个等腰梯形 |
| C.两个直角三角形,一个等腰三角形 | D.都是等边三角形 |
如图,□ABCD的周长为16cm,AC、BD相交于点 O, OE⊥AC交AD于E,则△DCE的周长为( )(考查平行四边形的性质)
A.4cm
B.6cm
C.8cm
D.10cm
下列四个命题中,假命题的是( ).(考查特殊四边形的判定)
| A.有三个角是直角的四边形是矩形; |
| B.对角线互相垂直平分且相等的四边形是正方形; |
| C.四条边都相等的四边形是菱形; |
| D.顺次连接等腰梯形各边中点,得到一个矩形 |
如图,在平行四边形ABCD中,AB在x轴上,D点y轴上, ,
, ,B点坐标为(4,0).点
,B点坐标为(4,0).点 是边
是边 上一点,且
上一点,且 .点
.点 、
、 分别从
分别从 、
、 同时出发,以1厘米/秒的速度分别沿
同时出发,以1厘米/秒的速度分别沿 、
、 向点
向点 运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为
运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为 ,设运动时间为
,设运动时间为 秒。
秒。
求直线BC的解析式。
当
 为何值时,
为何值时, ?
?在(2)问条件下,⊙E与直线PF是否相切;如果相切,加以证明,并求出切点的坐标。如果不相切,说明理由。
在梯形ABCD中,AB∥CD,∠BCD=90,且AB=1,BC=2,tan∠ADC=2;对角线相交于O点,等腰直角三角板的直角顶点落在梯形的顶点C上,使三角板绕点C旋转。
当三角板旋转到图1的位置时,猜想DE与BF的数量关系,并加以证明。
在(1)问条件下,若BE:CE=1:2,∠BEC=135°,求sin∠BFE的值。
当三角板的一边CF与梯形对角线AC重合时,作DH⊥PE于H,如图2,若OF=
 时,求PE及DH的长。
时,求PE及DH的长。
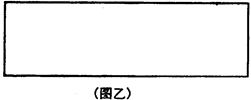
四年一度的国际数学家大会会标如图甲.它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.现有一张长为6.5cm、宽为2cm的纸片,如图乙,请你根据图甲的启示将它分割成6块,再拼合成一个正方形.(要求:先在图乙中画出分割线,再画出拼成的正方图甲形并标明相应数据)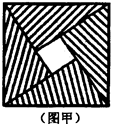
如图,网络中每个小正方形的边长为1,点 的坐标为
的坐标为

画出直角坐标系(要求标出
 轴,
轴, 轴和原点)并写出点
轴和原点)并写出点 的坐标;
的坐标;以
 为基本图形,利用轴对称或旋转或平移设计一个图案,说明你的创意
为基本图形,利用轴对称或旋转或平移设计一个图案,说明你的创意
如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积为 .
用边长为1cm的小正方形搭如下的塔状图形,则第n次所搭图形的周长是_ cm(用含n的代数式表示).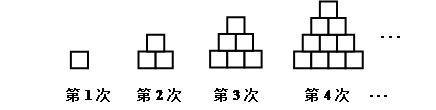
在矩形ABCD中,AB=5,BC=12,⊙A的半径为2,若以C为圆心作一个圆,使⊙C与⊙A相切,那么⊙C的半径为 。
已知,正方形ABCD,点P在对角线BD上,连接AP、CP(如图①)
(1)求证:AP=CP.
(2)将一直角三角板的直角顶点置于点P处并绕点P旋转,设两直角边分别交DC、BC于E、F,
a.若旋转到图②位置,使PE与PA在一直线上,求证:PF=PA.
b.若旋转到图③位置且PD∶PB=2∶3,求PE∶PF的值.