初中数学四边形综合题解答题

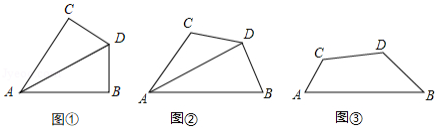
如图①，是矩形的对角线，，．将沿射线方向平移到△的位置，使为中点，连接，，，，如图②．

（1）求证：四边形是菱形；

（2）四边形的周长为　　；

（3）将四边形沿它的两条对角线剪开，用得到的四个三角形拼成与其面积相等的矩形，直接写出所有可能拼成的矩形周长．

【再现】如图①，在中，点，分别是，的中点，可以得到：，且．（不需要证明）

【探究】如图②，在四边形中，点，，，分别是，，，的中点，判断四边形的形状，并加以证明．

【应用】在（1）【探究】的条件下，四边形中，满足什么条件时，四边形是菱形？你添加的条件是：　　．（只添加一个条件）

（2）如图③，在四边形中，点，，，分别是，，，的中点，对角线，相交于点．若，四边形面积为5，则阴影部分图形的面积和为　　．

感知：如图1，平分．，，易知：．

探究：如图2，平分，，，求证：．

应用：如图3，四边形中，，，，则　　（用含的代数式表示）

平面内，如图，在中，，，，点为边上任意点，连接，将绕点逆时针旋转得到线段．

（1）当时，求的大小；

（2）当时，求点与点间的距离（结果保留根号）；

（3）若点恰好落在的边所在的直线上，直接写出旋转到所扫过的面积．（结果保留

如图，△ABC中，点E、P在边AB上，且AE=BP，过点E、P作BC的平行线，分别交AC于点F、Q．记△AEF的面积为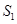，四边形EFQP的面积为，四边形PQCB的面积为

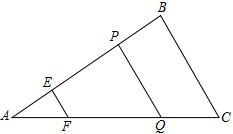
（1）求证：EF＋PQ=BC
（2）若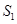＋=，求的值
（3）若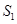－=，直接写出的值

（年新疆、生产建设兵团）如图，四边形ABCD为菱形，点E为对角线AC上的一个动点，连结DE并延长交AB于点F，连结BE．
（1）如图①，求证：∠AFD=∠EBC；
（2）如图②，若DE=EC且BE⊥AF，求∠DAB的度数；
（3）若∠DAB=90°且当△BEF为等腰三角形时，求∠EFB的度数（只写出条件与对应的结果）