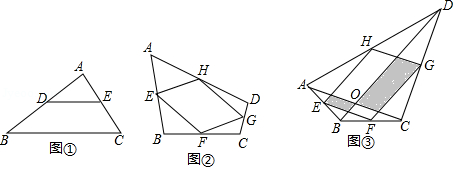
【再现】如图①,在中,点,分别是,的中点,可以得到:,且.(不需要证明)
【探究】如图②,在四边形中,点,,,分别是,,,的中点,判断四边形的形状,并加以证明.
【应用】在(1)【探究】的条件下,四边形中,满足什么条件时,四边形是菱形?你添加的条件是: .(只添加一个条件)
(2)如图③,在四边形中,点,,,分别是,,,的中点,对角线,相交于点.若,四边形面积为5,则阴影部分图形的面积和为 .
推荐套卷
【再现】如图①,在中,点,分别是,的中点,可以得到:,且.(不需要证明)
【探究】如图②,在四边形中,点,,,分别是,,,的中点,判断四边形的形状,并加以证明.
【应用】在(1)【探究】的条件下,四边形中,满足什么条件时,四边形是菱形?你添加的条件是: .(只添加一个条件)
(2)如图③,在四边形中,点,,,分别是,,,的中点,对角线,相交于点.若,四边形面积为5,则阴影部分图形的面积和为 .
