如图,在平面直角坐标系中,矩形 AOCB的两边 OA、 OC分别在 x轴和 y轴上,且 OA=2, OC=1.在第二象限内,将矩形 AOCB以原点 O为位似中心放大为原来的 倍,得到矩形 A 1 OC 1 B 1,再将矩形 A 1 OC 1 B 1以原点 O为位似中心放大 倍,得到矩形 A 2 OC 2 B 2…,以此类推,得到的矩形 A n O∁ n B n的对角线交点的坐标为 .

如图所示,在矩形ABCD中, ,点E是CD上一点,BE交AC于点F,将△BCE沿BE折叠,点C恰好落在AB边上的点C′处,则 .
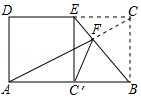
如图,在矩形 ABCD中, AD=8,对角线 AC与 BD相交于点 O, AE⊥ BD,垂足为点 E,且 AE平分∠ BAC,则 AB的长为 .
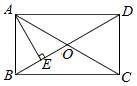
如图,在矩形 ABCD中, AB=8, BC=6, M为 AD上一点,将△ ABM沿 BM翻折至△ EBM, ME和 BE分别与 CD相交于 O, F两点,且 OE= OD,则 AM的长为 .

以矩形 ABCD两条对角线的交点 O为坐标原点,以平行于两边的方向为坐标轴,建立如图所示的平面直角坐标系, BE⊥ AC,垂足为 E.若双曲线 y=( x>0)经过点 D,则 OB• BE的值为 .

如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP= .
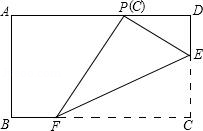
如图所示,反比例函数 y= ( x<0)的图象经过矩形 OABC的对角线 AC的中点 M,分别与 AB, BC交于点 D、 E,若 BD=3, OA=4,则 k的值为 .

如图,在矩形 ABCD中,点 E是 CD的中点,点 F是 BC上一点,且 FC=2 BF,连接 AE, EF.若 AB=2, AD=3,则cos∠ AEF的值是 .

如图,在一张矩形纸片 ABCD中, AB=3,点 P, Q分别是 AB和 CD的中点,现将这张纸片折叠,使点 D落到 PQ上的点 G处,折痕为 CH,若 HG的延长线恰好经过点 B,则 AD的长为 .
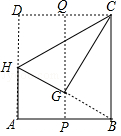
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在点A′的位置,若 , ,则点A′的坐标为 .

已知矩形ABCD的四个顶点均在反比例函数 的图象上,且点A的横坐标是2,则矩形ABCD的面积为 .
如图,在矩形 中,
中, ,以顶点
,以顶点 为圆心,1为半径作
为圆心,1为半径作 ,过边
,过边 上的一点
上的一点 作射线
作射线 与
与 相切于点
相切于点 ,且交边
,且交边 于点
于点 ,连接
,连接 ,若
,若 ,
, ,则
,则 的大小约为 度 分.(参考数据:
,
)
的大小约为 度 分.(参考数据:
,
)

如图,矩形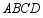 中,
中,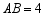 ,
, ,
,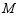 是边
是边 上一点,将
上一点,将 沿直线
沿直线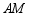 对折,得到
对折,得到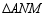 .
.
(1)当 平分
平分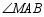 时,求
时,求 的长;
的长;
(2)连接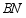 ,当
,当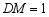 时,求
时,求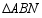 的面积;
的面积;
(3)当射线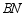 交线段
交线段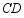 于点
于点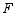 时,求
时,求 的最大值.
的最大值.
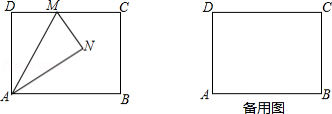
如图,矩形纸片  中,
中,  ,
,  ,先按图(2)操作:将矩形纸片
,先按图(2)操作:将矩形纸片  沿过点
沿过点  的直线折叠,使点
的直线折叠,使点  落在边
落在边  上的点
上的点  处,折痕为
处,折痕为  ;再按图(3)操作,沿过点
;再按图(3)操作,沿过点  的直线折叠,使点
的直线折叠,使点  落在
落在  上的点
上的点  处,折痕为
处,折痕为  ,则
,则  、
、  两点间的距离为 .
两点间的距离为 .
