如图,在矩形纸片 中, ,点 在边 上,将 沿直线 折叠,点 恰好落在对角线 上的点 处,若 ,则 的长是

A. B.4C.5D.6
如图,在矩形 中,点 在 上,将矩形沿 折叠,使点 落在 边上的点 处.若 , ,则 的值为

A. B. C. D.
如图,矩形 的四个顶点分别在直线 , , , 上.若直线 且间距相等, , ,则 的值为

A. B. C. D.
如图,矩形 中, , 相交于点 ,过点 作 交 于点 ,交 于点 ,过点 作 交 于点 ,交 于点 ,连接 , .则下列结论:
① ;
② ;
③ ;
④当 时,四边形 是菱形.
其中,正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展平后再次折叠,使点 落在 上的点 处,得到折痕 , 与 相交于点 .若直线 交直线 于点 , , ,则 的长为
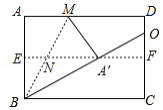
A. B. C. D.
把一张宽为 的长方形纸片 折叠成如图所示的阴影图案,顶点 , 互相重合,中间空白部分是以 为直角顶点,腰长为 的等腰直角三角形,则纸片的长 (单位: 为

A. B. C. D.
如图,点 为矩形 的对称中心,点 从点 出发沿 向点 运动,移动到点 停止,延长 交 于点 ,则四边形 形状的变化依次为

A.平行四边形 正方形 平行四边形 矩形
B.平行四边形 菱形 平行四边形 矩形
C.平行四边形 正方形 菱形 矩形
D.平行四边形 菱形 正方形 矩形
七巧板是我国祖先的一项卓越创造,流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板,如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形,则这两个图形中,中国七巧板和日本七巧板能拼成的个数分别是

A.1和1B.1和2C.2和1D.2和2
如图,在矩形 中, , ,点 、 在 边上, 和 交于点 ,若 ,则图中阴影部分的面积为
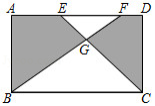
A.25B.30C.35D.40
如图,在平面直角坐标系中,矩形 的对角线 的中点与坐标原点重合,点 是 轴上一点,连接 .若 平分 ,反比例函数 的图象经过 上的两点 , ,且 , 的面积为18,则 的值为

A.6B.12C.18D.24
如图,已知点 是矩形 的对角线 上的一动点,正方形 的顶点 、 都在边 上,若 , ,则 的值

A.等于 B.等于
C.等于 D.随点 位置的变化而变化
如图,矩形 中, , , 为边 上一个动点,连接 ,取 的中点 ,点 绕点 逆时针旋转 得到点 ,连接 ,则 面积的最小值是

A.4B. C.3D.
如图,矩形 中, 是 的中点,将 沿 翻折,点 落在点 处, .设 , 的面积为 ,则 与 的函数图象大致为

A. B.
B.
C.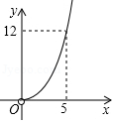 D.
D.
如图,将矩形 沿 折叠,点 落在点 处,点 落在 边上的点 处,若 ,则 等于
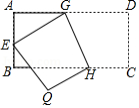
A. B. C. D.