初中数学菱形的性质试题

如图，矩形 $\mathit{ABCD}$与菱形 $\mathit{EFGH}$的对角线均交于点 $O$，且 $\mathit{EG}//\mathit{BC}$，将矩形折叠，使点 $C$与点 $O$重合，折痕 $\mathit{MN}$恰好过点 $G$若 $\mathit{AB}=\sqrt{6}$， $\mathit{EF}=2$， $\angle H=120°$，则 $\mathit{DN}$的长为 $($　　 $)$

A． $\frac{\sqrt{3}}{2}$B． $\frac{\sqrt{6}+\sqrt{3}}{2}$C． $\sqrt{6}-\sqrt{3}$D． $2\sqrt{3}-\sqrt{6}$

如图，已知菱形 $\mathit{ABCD}$的边长为4， $\angle \mathit{ABC}=60°$，对角线 $\mathit{AC}$、 $\mathit{BD}$相交于点 $O$，则菱形 $\mathit{ABCD}$的面积是　　．

如图，在菱形 $\mathit{ABCD}$中，对角线 $\mathit{AC}$与 $\mathit{BD}$相交于点 $O$， $\mathit{AC}=8$， $\mathit{BD}=6$， $\mathit{OE}\perp \mathit{BC}$，垂足为点 $E$，则 $\mathit{OE}=$　　．

如图，菱形 $\mathit{ABCD}$的周长是 $8\mathit{cm}$， $\mathit{AB}$的长是　　 $\mathit{cm}$．

如图，点 $E$，点 $F$分别在菱形 $\mathit{ABCD}$的边 $\mathit{AB}$， $\mathit{AD}$上，且 $\mathit{AE}=\mathit{DF}$， $\mathit{BF}$交 $\mathit{DE}$于点 $G$，延长 $\mathit{BF}$交 $\mathit{CD}$的延长线于 $H$，若 $\frac{\mathit{AF}}{\mathit{DF}}=2$，则 $\frac{\mathit{HF}}{\mathit{BG}}$的值为 $($　　 $)$

A． $\frac{2}{3}$B． $\frac{7}{12}$C． $\frac{1}{2}$D． $\frac{5}{12}$

如图，四边形 $\mathit{ABCD}$是菱形， $\mathit{CE}\perp \mathit{AB}$交 $\mathit{AB}$的延长线于点 $E$， $\mathit{CF}\perp \mathit{AD}$交 $\mathit{AD}$的延长线于点 $F$，求证： $\mathit{DF}=\mathit{BE}$．

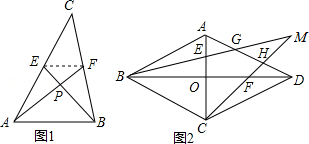
尤秀同学遇到了这样一个问题：如图1所示，已知AF，BE是△ABC的中线，且 $\mathit{AF}\perp \mathit{BE}$，垂足为P，设 $\mathit{BC}＝a，\mathit{AC}＝b，\mathit{AB}＝c$．

求证： $a^2+b^2＝5c^2$

该同学仔细分析后，得到如下解题思路：

先连接EF，利用EF为△ABC的中位线得到△EPF∽△BPA，故 $\frac{\mathit{EP}}{\mathit{BP}}=\frac{\mathit{PF}}{\mathit{PA}}=\frac{\mathit{EF}}{\mathit{BA}}=\frac{1}{2}$，设 $\mathit{PF}＝m，\mathit{PE}＝n$，用m，n把PA，PB分别表示出来，再在Rt△APE，Rt△BPF中利用勾股定理计算，消去m，n即可得证

（1）请你根据以上解题思路帮尤秀同学写出证明过程．

（2）利用题中的结论，解答下列问题：

在边长为3的菱形ABCD中，O为对角线AC，BD的交点，E，F分别为线段AO，DO的中点，连接BE，CF并延长交于点M，BM，CM分别交AD于点G，H，如图2所示，求 $M{G}^2+M{H}^2$的值．

如图，在菱形 ABCD中， $\angle \mathit{BAD}＝120°$ ，点 E、 F分别在边 AB、 BC上，△ BEF与△ GEF关于直线 EF对称，点 B的对称点是点 G，且点 G在边 AD上．若 $\mathit{EG}\perp \mathit{AC}$ ， $\mathit{AB}＝6\sqrt{2}$ ，则 FG的长为 　　．

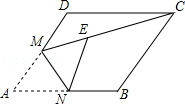
如图，在边长为2的菱形 ABCD中，∠ A＝60°，点 M是 AD边的中点，连接 MC，将菱形 ABCD翻折，使点 A落在线段 CM上的点 E处，折痕交 AB于点 N，则线段 EC的长为 　　．

如图，在菱形 ABCD中， G是 BD上一点，连接 CG并延长交 BA的延长线于点 F，交 AD于点 E．

（1）求证： AG＝ CG．

（2）求证： AG ²＝ GE• GF．

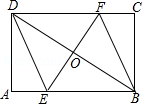
如图，矩形ABCD中，AB＝6，BC＝4，过对角线BD中点O的直线分别交AB，CD边于点E，F．

（1）求证：四边形BEDF是平行四边形；

（2）当四边形BEDF是菱形时，求EF的长．

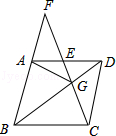
已知菱形 ABCD， E、 F是动点，边长为4， BE＝ AF，∠ BAD＝120°，则下列结论正确的有几个（　　）

①△ BEC≌△ AFC；②△ ECF为等边三角形；③∠ AGE＝∠ AFC；④若 AF＝1，则 $\frac{\mathit{GF}}{\mathit{EG}}$ ＝ $\frac{1}{3}$ ．

A．

1

B．

2

C．

3

D．

4

如图， BD是菱形 ABCD的对角线，∠ CBD＝75°，

（1）请用尺规作图法，作 AB的垂直平分线 EF，垂足为 E，交 AD于 F；（不要求写作法，保留作图痕迹）

（2）在（1）条件下，连接 BF，求∠ DBF的度数．

如图，点 P是菱形 ABCD边上的一动点，它从点 A出发沿在 A→ B→ C→ D路径匀速运动到点 D，设△ PAD的面积为 y， P点的运动时间为 x，则 y关于 x的函数图象大致为（　　）

A．		B．
C．		D．

如图，若菱形 ABCD的顶点 A， B的坐标分别为（3，0），（﹣2，0），点 D在 y轴上，则点 C的坐标是 　　．