如图,在菱形 ABCD中, ,点 E、 F分别在边 AB、 BC上,△ BEF与△ GEF关于直线 EF对称,点 B的对称点是点 G,且点 G在边 AD上.若 , ,则 FG的长为 .

如图,菱形 中,对角线 , 相交于点 , , ,动点 从点 出发,沿线段 以 的速度向点 运动,同时动点 从点 出发,沿线段 以 的速度向点 运动,当其中一个动点停止运动时另一个动点也随之停止.设运动时间为 ,以点 为圆心, 长为半径的 与射线 ,线段 分别交于点 , ,连接 .
(1)求 的长(用含有 的代数式表示),并求出 的取值范围;
(2)当 为何值时,线段 与 相切?
(3)若 与线段 只有一个公共点,求 的取值范围.

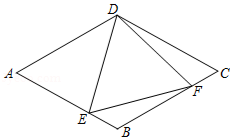
如图,在菱形 ABCD中, G是 BD上一点,连接 CG并延长交 BA的延长线于点 F,交 AD于点 E.
(1)求证: AG= CG.
(2)求证: AG 2= GE• GF.
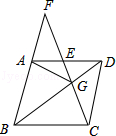
如图,菱形 中, ,点 从点 出发,沿折线 方向移动,移动到点 停止.在 形状的变化过程中,依次出现的特殊三角形是
| A. |
直角三角形 等边三角形 等腰三角形 直角三角形 |
| B. |
直角三角形 等腰三角形 直角三角形 等边三角形 |
| C. |
直角三角形 等边三角形 直角三角形 等腰三角形 |
| D. |
等腰三角形 等边三角形 直角三角形 等腰三角形 |
已知菱形 ABCD, E、 F是动点,边长为4, BE= AF,∠ BAD=120°,则下列结论正确的有几个( )
①△ BEC≌△ AFC;②△ ECF为等边三角形;③∠ AGE=∠ AFC;④若 AF=1,则 = .

| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
点 、 为半径是3的圆周上两点,点 为 的中点,以线段 、 为邻边作菱形 ,顶点 恰在该圆直径的三等分点上,则该菱形的边长为
A. 或 B. 或 C. 或 D. 或
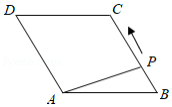
如图,点 P是菱形 ABCD边上的一动点,它从点 A出发沿在 A→ B→ C→ D路径匀速运动到点 D,设△ PAD的面积为 y, P点的运动时间为 x,则 y关于 x的函数图象大致为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
在菱形 中, ,在同一平面内,以对角线 为底边作顶角为 的等腰三角形 ,则 的度数为 .
如图,在菱形 中,对角线 , ,分别以点 , , , 为圆心, 的长为半径画弧,与该菱形的边相交,则图中阴影部分的面积为 .(结果保留

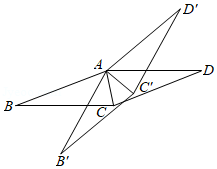
如图.将菱形 绕点 逆时针旋转 得到菱形 , .当 平分 时, 与 满足的数量关系是
| A. |
|
B. |
|
C. |
|
D. |
|
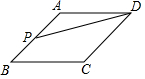
如图,在菱形 中, ,点 , 分别在边 , 上, , 的周长为 ,则 的长为
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在直角坐标系中,菱形 的顶点 , , 在坐标轴上,若点 的坐标为 , ,则点 的坐标为

| A. |
|
B. |
, |
C. |
|
D. |
|
如图,在菱形 中, , ,点 在边 上,且 .若直线 经过点 ,将该菱形的面积平分,并与菱形的另一边交于点 ,则线段 的长为 .

如图,在平面直角坐标系 中,菱形 的边长为2,点 在第一象限,点 在 轴正半轴上, ,若将菱形 绕点 顺时针旋转 ,得到四边形 ,则点 的对应点 的坐标为 .
