如图,在等腰 中, , ,点 为 的中点,点 , 分别是线段 , 上的动点,且 ,若 的长为 ,则 的周长是 (用含 的代数式表示).

如图,在 中, , , ,分别以点 , 为圆心,大于线段 长度一半的长为半径作弧,相交于点 , ,过点 , 作直线 ,交 于点 ,连接 ,则 的长是 .
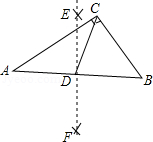
如图, 是 的直径, ,点 是 的中点,过点 的直线与 交于 、 两点.若 ,则弦 的长为 .

我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点 到以原点为圆心,以1为半径的圆的距离为 .

在 中, , , ,点 在 的边上,且 ,将 折叠,使点 落在点 处,折痕交边 于点 ,交另一边于点 ,则 .
如图,在 中, , , ,点 在线段 上,且 , 是线段 上的一点,连接 ,把四边形 沿直线 翻折,得到四边形 ,当点 恰好落在线段 上时, .

如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么 的值为 .

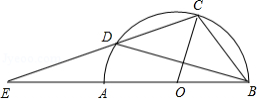
如图,半圆的半径 ,线段 与 是半圆的两条弦, ,延长 交直径 的延长线于点 ,若 ,则弦 的长为 .
如图,在 中, , , 、 分别在 、 上,点 在 内.若四边形 是边长为1的正方形,则 .

如图,在边长为 的正方形 中,点 , 分别是边 , 的中点,连接 , ,点 , 分别是 , 的中点,连接 ,则 的长度为 .
