勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出

| A. |
直角三角形的面积 |
| B. |
最大正方形的面积 |
| C. |
较小两个正方形重叠部分的面积 |
| D. |
最大正方形与直角三角形的面积和 |
在数学拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积.如图是由5个边长为1的小正方形拼成的图形, 是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点 的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, 是 边上的中点,连结 ,把 沿 翻折,得到 , 与 交于点 ,连结 ,若 , ,则点 到 的距离为

| A. |
|
B. |
|
C. |
|
D. |
|
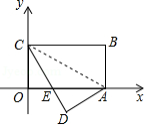
如图,矩形 的边 在 轴上, , ,把 沿直线 折叠,得到 , 交 轴于点 ,则点 的坐标是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,四边形 为菱形, , 两点的坐标分别是 , ,点 , 在坐标轴上,则菱形 的周长等于

| A. |
|
B. |
|
C. |
|
D. |
20 |
如图,在 中, , , ,以 的中点 为圆心, 的长为半径作半圆交 于点 ,则图中阴影部分的面积为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知 ,点 、 在射线 上(点 在点 、 之间),半径长为2的 与直线 相切,半径长为3的 与 相交,那么 的取值范围是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在菱形 中.点 、 、 、 分别是边 、 、 和 的中点,连接 、 、 和 .若 ,则下列结论正确的是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , , , ,垂足为 , 的平分线交 于点 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
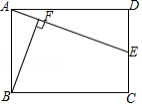
如图,在矩形 中, , .若点 是边 的中点,连接 ,过点 作 交 于点 ,则 的长为
| A. |
|
B. |
|
C. |
|
D. |
|
如图,将两个大小、形状完全相同的 和△ 拼在一起,其中点 与点 重合,点 落在边 上,连接 .若 , ,则 的长为

| A. |
|
B. |
6 |
C. |
|
D. |
|
如图,在正方形 中, .若以 边为底边向其形外作等腰直角 ,连接 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图, 在 中, , , . 若 是 的中位线, 延长 交 的外角 的平分线于点 ,则线段 的长为

| A. |
A . 7B . 8C . 9D . 10 |
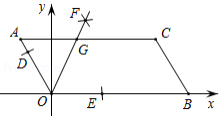
如图,已知的顶点
,
,点
在
轴正半轴上按以下步骤作图:①以点
为圆心,适当长度为半径作弧,分别交边
,
于点
,
;②分别以点
,
为圆心,大于
的长为半径作弧,两弧在
内交于点
;③作射线
,交边
于点
,则点
的坐标为
A.,
B.
,
C.
,
D.
,