如图,矩形纸片 中, , ,将 沿 折叠,使点 落在点 处, 交 于点 ,则 的长等于

A. B. C. D.
如图,在 中, , , 、 分别在 、 上,点 在 内.若四边形 是边长为1的正方形,则 .

如图,在 的方格纸 中,请按要求画格点线段(端点在格点上),且线段的端点均不与点 , , , 重合.

(1)在图1中画格点线段 , 各一条,使点 , , , 分别落在边 , , , 上,且 , 不平行 .
(2)在图2中画格点线段 , 各一条,使点 , , , 分别落在边 , , , 上,且 .
如图,在 中, , , 为 边的中点,线段 的垂直平分线交边 于点 .设 , ,则

A. B. C. D.
如图, 、 、 、 是四根长度均为 的火柴棒,点 、 、 共线.若 , ,则线段 的长度是

| A. |
|
B. |
|
C. |
|
D. |
|
如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形 中, , ,问四边形 是垂美四边形吗?请说明理由.
(2)性质探究:试探索垂美四边形 两组对边 , 与 , 之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证).
(3)问题解决:如图3,分别以 的直角边 和斜边 为边向外作正方形 和正方形 ,连接 , , ,已知 , ,求 长.

如图,已知边长为2的等边三角形 中,分别以点 , 为圆心, 为半径作弧,两弧交于点 ,连结 .若 的长为 ,则 的值为 .

如图,在 中, ,按以下步骤作图:①以 为圆心,任意长为半径作弧,分别交 、 于 、 两点;②分别以 、 为圆心,以大于 的长为半径作弧,两弧相交于点 ;③作射线 ,交边 于 点.若 , ,则线段 的长为

| A. |
3 |
B. |
|
C. |
|
D. |
|
如图,在 纸片中, , , ,点 , 分别在 , 上,连结 ,将 沿 翻折,使点 的对应点 落在 的延长线上,若 平分 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
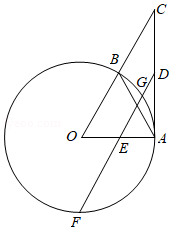
如图, , 是 上两点,且 ,连接 并延长到点 ,使 ,连接 .
(1)求证: 是 的切线;
(2)点 , 分别是 , 的中点, 所在直线交 于点 , , ,求 的长.