已知: AC是▱ ABCD的对角线.
(1)用直尺和圆规作出线段 AC的垂直平分线,与 AD相交于点 E,连接 CE.(保留作图痕迹,不写作法);
(2)在(1)的条件下,若 AB=3, BC=5,求△ DCE的周长.

如图,在△ABC中,按以下步骤作图:①分别以点A和点C为圆心,以大于 x(x-1)=21.AC的长为半径作弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD.若AB=BD,AB=6,∠C=30°,则△ACD的面积为 .

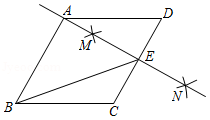
如图,在菱形 ABCD中,按以下步骤作图:
①分别以点 C和点 D为圆心,大于 CD为半径作弧,两弧交于点 M, N;
②作直线 MN,且 MN恰好经过点 A,与 CD交于点 E,连接 BE,
则下列说法错误的是( )
| A. |
∠ABC=60° |
B. |
S △ ABE=2S △ ADE |
| C. |
若AB=4,则BE= |
D. |
sin∠CBE= |
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( )

A.1B.2C.3D.4
如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=( )

A.50°B.100°C.120°D.130°
如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19cm,△ABD的周长为13cm,则AE的长为( )

A.3cmB.6cmC.12cmD.16cm
如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )

A.13B.15C.17D.19
如图,在△ ABC中,按以下步骤作图:①分别以 B, C为圆心,以大于 BC的长为半径作弧,两弧相交于 M, N两点;②作直线 MN交 AB于点 D,连接 CD,若 AC= CD,∠ B=35°,则∠ ACB的度数为( )

| A. |
70° |
B. |
73° |
C. |
75° |
D. |
78° |
如图,在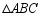 中,
中,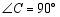 ,点
,点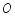 在
在 上,以
上,以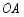 为半径的
为半径的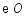 交
交 于点
于点 ,
,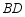 的垂直平分线交
的垂直平分线交 于点
于点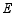 ,交
,交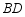 于点
于点 ,连接
,连接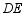 .
.
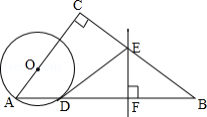
(1)判断直线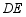 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若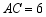 ,
, ,
,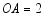 ,求线段
,求线段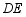 的长.
的长.
如图,在  中,
中,  .
.
(1)作边  的垂直平分线
的垂直平分线  ,与
,与  ,
,  分别相交于点
分别相交于点  ,
,  (用尺规作图,保留作图痕迹,不要求写作法);
(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接  ,若
,若  ,求
,求  的度数.
的度数.

如图,已知线段  ,分别以
,分别以  、
、  为圆心,大于
AB为半径作弧,连接弧的交点得到直线
为圆心,大于
AB为半径作弧,连接弧的交点得到直线  ,在直线
,在直线  上取一点
上取一点  ,使得
,使得  ,延长
,延长  至
至  ,求
,求  的度数为
的度数为 


| A. |
|
B. |
|
C. |
|
D. |
|
如图,在菱形ABCD中,AB=4,线段AD的垂直平分线交AC于点N,△CND的周长是10,则AC的长为 .

如图,在矩形ABCD中,AB=10,AD=6,点M为AB上的一动点,将矩形ABCD沿某一直线对折,使点C与点M重合,该直线与AB(或BC)、CD(或DA)分别交于点P、Q
(1)用直尺和圆规在图甲中画出折痕所在直线(不要求写画法,但要求保留作图痕迹)
(2)如果PQ与AB、CD都相交,试判断△MPQ的形状并证明你的结论;
(3)设AM=x,d为点M到直线PQ的距离,y=d2,
①求y关于x的函数解析式,并指出x的取值范围;
②当直线PQ恰好通过点D时,求点M到直线PQ的距离.

如图, 中, , 是 的平分线, 是 的垂直平分线,交 于点 .若 ,则 外接圆的面积为

| A. |
|
B. |
|
C. |
|
D. |
|