发现规律
(1)如图①, 与 都是等边三角形,直线 , 交于点 .直线 , 交于点 .求 的度数.
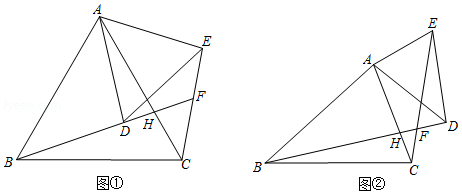
(2)已知: 与 的位置如图②所示,直线 , 交于点 .直线 , 交于点 .若 , ,求 的度数.
应用结论
(3)如图③,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 , 为 轴上一动点,连接 .将线段 绕点 逆时针旋转 得到线段 ,连接 , .求线段 长度的最小值.
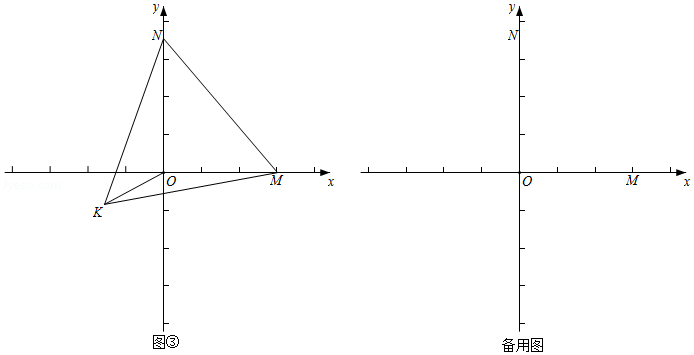
如图,在 中, ,以 为直径的 与 相交于点 ,过点 作 的切线交 于点 .
(1)求证: ;
(2)若 的半径为5, ,求 的长.
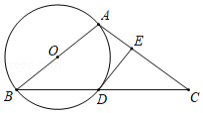
问题:如图,在 中, .在 的延长线上取点 , ,作 ,使 .若 , ,求 的度数.
答案: .
思考:(1)如果把以上“问题”中的条件“ ”去掉,其余条件不变,那么 的度数会改变吗?说明理由.
(2)如果把以上“问题”中的条件“ ”去掉,再将“ ”改为“ ”,其余条件不变,求 的度数.
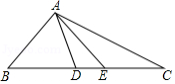
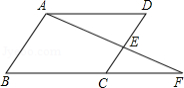
如图,点 是 的边 的中点,连结 并延长,交 的延长线于点 .
(1)若 的长为2,求 的长.
(2)若 ,试添加一个条件,并写出 的度数.
如图,已知 是 的直径,半径 ,点 在劣弧 上(不与点 ,点 重合), 与 交于点 .设 , ,则

A. B. C. D.
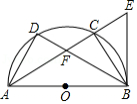
如图, 是半圆 的直径, , 是半圆 上不同于 , 的两点, , 与 相交于点 . 是半圆 所在圆的切线,与 的延长线相交于点 .
(1)求证: ;
(2)若 ,求证: 平分 .
等腰三角形的一个内角为 ,则另外两个内角的度数分别是
A. , B. , 或 ,
C. , D. , 或 ,
如图,在 中, ,分别以点 、 为圆心,以大于 的长为半径画弧,两弧分别交于点 、 ,作直线 交 点 ;以点 为圆心,适当长为半径画弧,分别交 、 于点 、 ,再分别以点 、 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 ,此时射线 恰好经过点 ,则 度.

如图摆放的一副学生用直角三角板, , , 与 相交于点 ,当 时, 的度数是

A. B. C. D.