初中数学三角形三边关系试题

下列长度的三条线段，能组成三角形的是 $($ 　　 $)$

A．

3，4，8

B．

5，6，10

C．

5，5，11

D．

5，6，11

若长度分别为 $a$ ，3，5的三条线段能组成一个三角形，则 $a$ 的值可以是 $($ 　　 $)$

A．

1

B．

2

C．

3

D．

8

数学课上，李老师准备了四张背面看上去无差别的卡片，，，，每张卡片的正面标有字母，，表示三条线段（如图），把四张卡片背面朝上放在桌面上，李老师从这四张卡片中随机抽取一张卡片后不放回，再随机抽取一张．

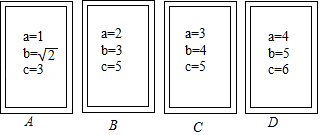
（1）用树状图或者列表表示所有可能出现的结果；

（2）求抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率．

下列说法正确的是 $($ 　　 $)$

A．	$A$ ．垂直于直径的弦平分这条直径
B．	$B$ ．负数没有立方根
C．	$C$ ．两条对角线互相垂直的四边形是菱形
D．	$D$ ．三角形两边的差小于第三边

等腰三角形的两边分别为3和6，则这个三角形的周长是 $($ 　　 $)$

A．

9

B．

12

C．

15

D．

12或15

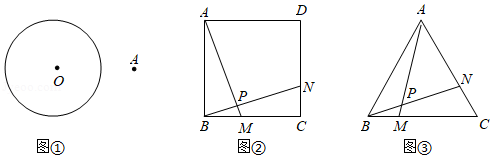
（1）如图①，点是外一点，点是上一动点．若的半径为3，且，则点到点的最短距离为　 ；

（2）如图②，已知正方形的边长为4，点、分别从点、同时出发，以相同的速度沿边、方向向终点和运动，连接和交于点，则点到点的最短距离为　　；

（3）如图③，在等边中，，点、分别从点、同时出发，以相同的速度沿边、方向向终点和运动，连接和交于点，求面积的最大值，并说明理由．

问题提出

（1）如图①，在 $\mathit{\Delta ABC}$ 中， $\mathit{BC}=6$ ， $D$ 为 $\mathit{BC}$ 上一点， $\mathit{AD}=4$ ，则 $\mathit{\Delta ABC}$ 面积的最大值是 　　．

问题探究

（2）如图②，已知矩形 $\mathit{ABCD}$ 的周长为12，求矩形 $\mathit{ABCD}$ 面积的最大值．

问题解决

（3）如图③， $\mathit{\Delta ABC}$ 是葛叔叔家的菜地示意图，其中 $\mathit{AB}=30$ 米， $\mathit{BC}=40$ 米， $\mathit{AC}=50$ 米，现在他想利用周边地的情况，把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地，用来建鱼塘．已知葛叔叔欲建的鱼塘是四边形 $\mathit{ABCD}$ ，且满足 $\angle \mathit{ADC}=60°$ ．你认为葛叔叔的想法能否实现？若能，求出这个四边形鱼塘周长的最大值；若不能，请说明理由．

以3、4为两边的三角形的第三边长是方程的根，则这个三角形的周长为（  ）

A．15或12

B．12

C．15

D．以上都不对

等腰三角形中，已知两边的长分别是9和5，则周长为__________．

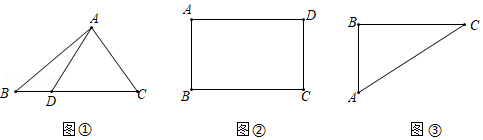
如图，P为等腰△ABC的顶角A的外角平分线上任一点，连接PB，PC．

（1）求证：PB+PC＞2AB．
（2）当PC=2，PB=，∠ACP=45°时，求AB的长．

已知三角形两边的长分别是4和10，则此三角形第三边的长可能是（  ）

A．5

B．6

C．11

D．16

已知等腰三角形的两边长分别为6cm、3cm，则该等腰三角形的周长是（  ）

A．9cm

B．12cm

C．12cm或15cm

D．15cm

以下列各组线段为边，能组成三角形的是（  ）

A．2，3，5

B．3，3，6

C．2，5，8

D．4，5，6

（年青海省中考）已知三角形两边的长分别是4和10，则此三角形第三边的长可能是（ ）

A．5

B．6

C．12

D．16