如图,点 、 在反比例函数 的图象上,延长 交 轴于 点,若 的面积是12,且点 是 的中点,则 .

如图,等腰 的底边 ,面积为120,点 在边 上,且 , 是腰 的垂直平分线,若点 在 上运动,则 周长的最小值为 .
圆锥的底面周长为 ,母线长为2,点 是母线 的中点,一根细绳(无弹性)从点 绕圆锥侧面一周回到点 ,则细绳的最短长度为 .
如图,在边长为 的正方形 中,点 , 分别是边 , 的中点,连接 , ,点 , 分别是 , 的中点,连接 ,则 的长度为 .

如图,在 中, , , ,以点 为原点建立平面直角坐标系,使 在 轴正半轴上,点 是 边上的一个动点, 交 于 , 于 , 于 .以下结论:
① ;
②当 为 的中点时, ;
③点 的坐标为 ;
④将 沿 所在的直线翻折到原来的平面,点 的对应点 的坐标为 ;
⑤矩形 的最大面积为3.在这些结论中正确的有 (只填序号)

如图, 中,点 为边 的中点,连接 ,将 沿直线 翻折至 所在平面内,得 ,连接 ,分别与边 交于点 ,与 交于点 .若 , ,则 的长为 .

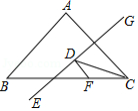
如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到△ ,使点 落在 上,边 交线段 于点 .若 ,则
度.
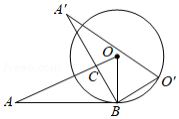
图1是一种矩形时钟,图2是时钟示意图,时钟数字2的刻度在矩形 的对角线 上,时钟中心在矩形 对角线的交点 上.若 ,则 长为 (结果保留根号).
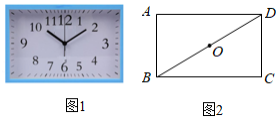
如图,在河对岸有一矩形场地 ,为了估测场地大小,在笔直的河岸 上依次取点 , , ,使 , ,点 , , 在同一直线上.在 点观测 点后,沿 方向走到 点,观测 点发现 .测得 米, 米, 米, ,则场地的边 为 米, 为 米.
