(年新疆、生产建设兵团)如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连结DE并延长交AB于点F,连结BE.
(1)如图①,求证:∠AFD=∠EBC;
(2)如图②,若DE=EC且BE⊥AF,求∠DAB的度数;
(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数(只写出条件与对应的结果)
(年江西省南昌市)我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.
特例探索
(1)如图1,当∠ABE=45°,c= 时,a= ,b= .
时,a= ,b= .
如图2,当∠ABE=30°,c=4时,a= ,b= .
归纳证明
(2)请你观察(1)中的计算结果,猜想 ,
, ,
, 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
拓展应用
(3)如图4,在▱ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD= ,AB=3,求AF的长.
,AB=3,求AF的长.

(年贵州省遵义市)在Rt△ABC中,∠BAC= ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD的面积.
(年蒙自市初中学业水平第一次模拟测试)已知 垂直平分
垂直平分 ,
, ,
, ,
,
(1)证明 是平行四边形;
是平行四边形;
(2)若 ,
, ,求
,求 的长.
的长.
(年新疆乌鲁木齐市)如图,▱ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.
(1)求证:四边形BEDF是平行四边形;
(2)若AB⊥AC,AB=4,BC= ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长.
(年云南省曲靖市)如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论.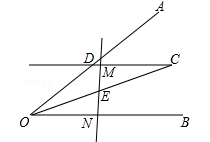
(年贵州省铜仁市)已知,如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD.
求证:AD=CE.
(年云南省昆明市)如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AC=DF.
(年云南省)如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.
(年贵州省遵义市)有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3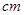 、7
、7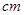 、9
、9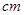 ;乙盒子中装有4张卡片,卡片上分别写着2
;乙盒子中装有4张卡片,卡片上分别写着2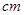 、4
、4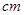 、6
、6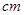 、8
、8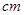 ;盒子外有一张写着5
;盒子外有一张写着5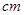 的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
(年贵州省黔东南州)如图,已知二次函数 的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为
的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为 .
.
(1)求二次函数 的解析式及点B的坐标;
的解析式及点B的坐标;
(2)由图象写出满足 的自变量x的取值范围;
的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出P的坐标;若不存在,说明理由.
(年青海省中考)如图,二次函数 的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由;
(3)探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角形与△BCM相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(本小题满分10分)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D
以AB上一点O为圆心作⊙O,使⊙O经过点A和点D。
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°,
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧 所围成的阴影部分的面积(结果保留根号和
所围成的阴影部分的面积(结果保留根号和 )。
)。
(贵州省安顺市)(本题12分)
如图,等腰三角形ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
(1)求证:直线EF是⊙O的切线;
(2)求 的值.
的值.