请阅读下列材料：若
是关于
的一元二次方程的两个根，则方程的两个根和系数
有如下关系：
． 我们把它们称为根与系数关系定理．
如果设二次函数
的图象与x轴的两个交点
．利用根与系数关系定理我们又可以得到A、B两个交点间的距离为：
请你参考以上定理和结论，解答下列问题：
设二次函数的图象与x轴的两个交点为，抛物线的顶点为
，显然
为等腰三角形。
（1）当为等腰直角三角形时，求
的值，
（2）当为等边三角形时，求的值，
（3）设抛物线
与
轴的两个交点为
、
，顶点为，且
，试问如何平移此抛物线，才能使
？
如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．
（1）求线段CD的长；
（2）当t为何值时，△CPQ与△ABC相似？
（3）当t为何值时，△CPQ为等腰三角形？
操作题：如图，△ABC内接于⊙O，AB=AC，P是⊙O上一点．
（1）请你只用无刻度的直尺，分别画出图①和图②中∠P的平分线；
（2）结合图②，说明你这样画的理由．
CD经过∠BCA顶点C的一条直线，CA=CB．E，F分别是直线CD上两点，且∠BEC=∠CFA=∠α．
（1）若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：
①如图1，若∠BCA=90°，∠α=90°，
则BE_____CF；EF_____|BE﹣AF|（填“＞”，“＜”或“=”）；
②如图2，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件__________，使①中的两个结论仍然成立，并证明两个结论成立．
（2）如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想（不要求证明）．
如图，在平行四边形ABCD中，AB＜BC．
（1）利用尺规作图，在BC边上确定点E，使点E到边AB，AD的距离相等（不写作法，保留作图痕迹）；
（2）若BC=8，CD=5，则CE= ．
如图，A、B、C三点在同一直线上，分别以AB、BC为边，在直线AC的同侧作等边△ABD和等边△BCE，连接AE交BD于点M，连接CD交BE于点N，连接MN得△BMN．
试判断△BMN的形状，并说明理由.
已知：在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．
（1）直线BF垂直于直线CE于点F，交CD于点G（如图①），求证：AE=CG；
（2）直线AH垂直于直线CE，垂足为点 H，交CD的延长线于点M（如图②），找出图中与BE相等的线段，并证明．
[问题提出]
学习了三角形全等的判定方法（即“SAS”，“ASA”，“AAS”，“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
[初步思考]我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E．然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．
[深入探究]
第一种情况：当∠B是直角时，△ABC≌△DEF．
（1）如图①，在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E＝90°，根据________，可以知道Rt△ABC≌Rt△DEF．
第二种情况：当∠B是钝角时，△ABC≌△DEF．
（2）如图②，在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B，∠E都是钝角．求证：△ABC≌△DEF．
第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
（3）在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B，∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）．
（4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接填写结论：
在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B，∠E都是锐角，若________，则△ABC≌△DEF．
如图，P为等腰△ABC的顶角A的外角平分线上任一点，连接PB，PC．
（1）求证：PB+PC＞2AB．
（2）当PC=2，PB=
，∠ACP=45°时，求AB的长．
如图是由边长都是1的小正方形组成的网格．请以图中线段BC为边，作△PBC，使P在格点上，并满足：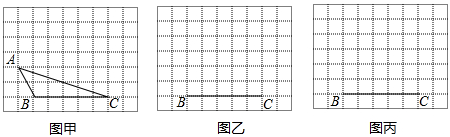
（1）图甲中的△PBC是直角三角形，且面积是△ABC面积2倍；
（2）图乙中的△PBC是等腰非直角三角形．
粤公网安备 44130202000953号
=
，求
的长．
，使
．（注：点C必须在格点上） 
在同一直线上，
，
，
∥
．求证：
．
