如图,在正方形 中, ,点 , 分别在边 , 上, .若将四边形 沿 折叠,点 恰好落在 边上,则 的长度为

| A. |
1 |
B. |
|
C. |
|
D. |
2 |
已知 的周长为16,点 , , 分别为 三条边的中点,则 的周长为
| A. |
8 |
B. |
|
C. |
16 |
D. |
4 |
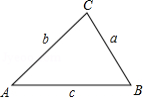
古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式,称为海伦 秦九韶公式:如果一个三角形的三边长分别是 , , ,记 ,那么三角形的面积为 .如图,在 中, , , 所对的边分别记为 , , ,若 , , ,则 的面积为
| A. |
|
B. |
|
C. |
18 |
D. |
|
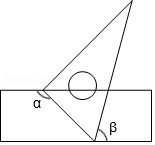
如图,将一块含有 角的直角三角板的两个顶点分别放在直尺的两条平行对边上,若 ,则 等于
| A. |
|
B. |
|
C. |
|
D. |
|
如图,正方形 中,点 、 分别在边 , 上, 与 交于点 .若 , ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图, 是 的直径, 是弦,四边形 是平行四边形, 与 相交于点 ,下列结论错误的是

| A. |
|
B. |
|
C. |
|
D. |
平分 |
勾股定理是"人类最伟大的十个科学发现之一".我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为"赵爽弦图" 年在北京召开的国际数学大会选它作为会徽.下列图案中是"赵爽弦图"的是
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 为 的直径, 为 的切线,弦 ,直线 交 的延长线于点 ,连接 .下列结论:① 是 的切线;② ;③ ;④ .其中正确结论的个数有

| A. |
4个 |
B. |
3个 |
C. |
2个 |
D. |
1个 |
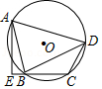
如图,四边形 内接于 , 交 的延长线于点 ,若 平分 , , ,则
| A. |
3 |
B. |
|
C. |
|
D. |
|
如图,矩形 的顶点 , , 分别落在 的边 , 上,若 ,要求只用无刻度的直尺作 的平分线.小明的作法如下:连接 , 交于点 ,作射线 ,则射线 平分 .有以下几条几何性质:①矩形的四个角都是直角,②矩形的对角线互相平分,③等腰三角形的"三线合一".小明的作法依据是

| A. |
①② |
B. |
①③ |
C. |
②③ |
D. |
①②③ |