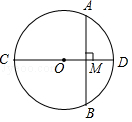
如图, CD为⊙ O的直径,弦 AB⊥ CD,垂足为 M,若 AB=12, OM: MD=5:8,则⊙ O的周长为( )
| A. |
26π |
B. |
13π |
C. |
|
D. |
|
如图,将半圆形纸片折叠,使折痕 CD与直径 AB平行, 的中点 P落在 OP上的点 P'处,且 OP'= OP,折痕 CD=2 ,则tan∠ COP的值为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在Rt△ ABC中,∠ C=90°,∠ B=30°,以 A为圆心适当长为半径画弧,分别交 AB、 AC于点 M、 N,分别以点 M、 N为圆心,大于 MN的长为半径画弧交于点 P,作射线 AP交 BC于点 D,再作射线 DE交 AB于点 E,则下列结论错误的是( )

| A. |
∠ADB=120° |
B. |
S △ ADC:S △ ABC=1:3 |
| C. |
若CD=2,则BD=4 |
D. |
DE垂直平分AB |
如图,将边长为4的菱形 ABCD纸片折叠,使点 A恰好落在对角线的交点 O处,若折痕 EF=2 ,则∠ A=( )

| A. |
120° |
B. |
100° |
C. |
60° |
D. |
30° |
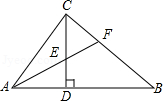
如图,在Rt△ ABC中,∠ ACB=90°, CD⊥ AB,垂足为 D, AF平分∠ CAB,交 CD于点 E,交 CB于点 F.若 AC=3, AB=5,则 CE的长为( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在△ ABC中, AB= AC,∠ ABC=45°,以 AB为直径的⊙ O交 BC于点 D,若 BC=4 ,则图中阴影部分的面积为( )

| A. |
π+1 |
B. |
π+2 |
C. |
2π+2 |
D. |
4π+1 |
若等腰三角形的周长为10 cm,其中一边长为2 cm,则该等腰三角形的底边长为( )
| A. |
2cm |
B. |
4cm |
C. |
6cm |
D. |
8cm |
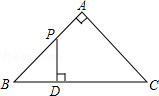
如图,Rt△ ABC中, AB=9, BC=6,∠ B=90°,将△ ABC折叠,使 A点与 BC的中点 D重合,折痕为 PQ,则线段 BQ的长度为( )

| A. |
|
B. |
|
C. |
4 |
D. |
5 |
如图,在△ ABC中, AB= AC,过点 A作 AD∥ BC,若∠1=70°,则∠ BAC的大小为( )

| A. |
40° |
B. |
30° |
C. |
70° |
D. |
50° |
如图,将矩形纸片 ABCD折叠,使点 B与点 D重合,折痕为 MN,若 AB=2, BC=4,那么线段 MN的长为( )

| A. |
|
B. |
|
C. |
|
D. |
2 |
如图,在△ ABC中,按以下步骤作图:①分别以 B, C为圆心,以大于 BC的长为半径作弧,两弧相交于 M, N两点;②作直线 MN交 AB于点 D,连接 CD,若 AC= CD,∠ B=35°,则∠ ACB的度数为( )

| A. |
70° |
B. |
73° |
C. |
75° |
D. |
78° |
等腰三角形有一个角是90°,则另两个角分别是( )
| A. |
30°,60° |
B. |
45°,45° |
C. |
45°,90° |
D. |
20°,70° |
如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )

A. B.
B.
C. D.
D.
如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A.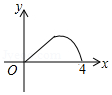 B.
B.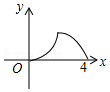
C.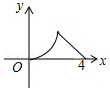 D.
D.