如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以 为圆心, 为半径画圆,选取的格点中除点 外恰好有3个在圆内,则 的取值范围为
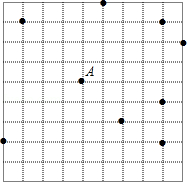
A. B. C. D.
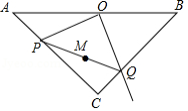
如图, , 两点被池塘隔开,在 外选一点 ,连接 , ,并分别找出它们的中点 , ,连接 ,现测得 ,则 长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,等腰 中,斜边 的长为2, 为 的中点, 为 边上的动点, 交 于点 , 为 的中点,当点 从点 运动到点 时,点 所经过的路线长为
A. B. C.1D.2
下列说法正确的是
| A. |
.垂直于直径的弦平分这条直径 |
| B. |
.负数没有立方根 |
| C. |
.两条对角线互相垂直的四边形是菱形 |
| D. |
.三角形两边的差小于第三边 |
如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 , 于点 , ,再分别以点 , 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 交边 于点 ,若 , ,则 的面积是
A.15B.30C.45D.60
如图,把含 的直角三角板 放置在正方形 中, ,直角顶点 在正方形 的对角线 上,点 , 分别在 和 边上, 与 交于点 ,且点 为 的中点,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
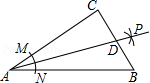
如图,点 , , , 共线, , ,添加一个条件,不能判断 的是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 纸片中, , , ,点 , 分别在 , 上,连结 ,将 沿 翻折,使点 的对应点 落在 的延长线上,若 平分 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形 组成,恰好拼成一个大正方形 .连结 并延长交 于点 .若 , ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在矩形 中,点 在 上,将矩形沿 折叠,使点 落在 边上的点 处.若 , ,则 的值为

A. B. C. D.
如图,等边三角形 边长是定值,点 是它的外心,过点 任意作一条直线分别交 , 于点 , .将 沿直线 折叠,得到△ ,若 , 分别交 于点 , ,连接 , ,则下列判断错误的是

A.
B.△ 的周长是一个定值
C.四边形 的面积是一个定值
D.四边形 的面积是一个定值
如图,等腰 中,点 , 分别在腰 , 上,添加下列条件,不能判定 的是

A. B. C. D.