初中数学平行线的性质试题

如图，把一张长方形的纸按图那样折叠后，B、D两点落在B′、D′点处，若∠BOG比∠AOB′小15°，则∠BOG的度数为      度．

如图，A、B、C、D四个点均在⊙O上，∠AOD=70°，AO∥DC，则∠B的度数为（  ）

A．40°           B．45°            C．50°         D．55°

用等腰直角三角板画∠AOB=45°，并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°，则三角板的斜边与射线OA的夹角α为______度．

如图，AB∥CD，直线EF分别交AB、CD于E、F，EG平分∠BEF，若∠1=70°，则∠2=           度．

如图，△ABC中，AB=5，AC=8，BD，CD分别平分∠ABC，∠ACB，过点D作直线平行于BC，交AB，AC于E，F，则△AEF的周长为（   ）

A．12

B．13

C．14

D．18

如图，在中，D、E分别是AB、AC上的点，点F在BC的延长线上，DE∥BC，，，则____________．

如图，从下列四个条件∠1+∠2=180°、∠2=∠3、∠1+∠3=180°、l₁∥l₂中选一个作为题设，一个作为结论，写出一个真命题为___________．

如图．等边△ABC中，∠ABC与∠ACB的平分线相交于点O，且OD∥AB，OE∥AC．


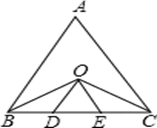
（1）试判定△ODE的形状．并说明你的理由；
（2）线段BD、DE、EC三者有什么关系？写出你的判断过程．

已知如图（1）：△ABC中，AB=AC，∠B、∠C的平分线相交于点O，过点O作EF∥BC分别交AB、AC于E、F．

（1）写出线段EF与BE、CF间的数量关系？（不证明）
（2）若AB≠AC，其他条件不变，如图（2），图中线段EF与BE、CF间是否存在（1）中数量关系？请说明理由．
（3）若△ABC中，AB≠AC，∠B的平分线与三角形外角∠ACD的平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F，如图（3），这时图中线段EF与BE，CF间存在什么数量关系？请说明理由．

直尺与三角尺按如图所示的方式叠放在一起，在图中所标记的角中，与∠1互余的角有几个（  ）

A．2个

B．3个

C．4个

D．6个

下面是某同学给出一种证法，请你将解答中缺少的条件、结论或证明理由补充完整：
证明：（已知）
∴（_________________________）
∵AB//CD（已知）
∴（ _______________________）
∵是的平分线，（已知）
∴_______（角平分线定义）
∵（已证）
∴（_________________）
∵_______________________（已证）
∴（等量代换）

如图，直线，被直线所截，∥，∠1=∠2，若∠3=40°，则∠4等于（  ）

A．40°

B．50°

C．70°

D．80°

如图，已知OB、OC为△ABC的角平分线，EF∥BC交AB、AC于E、F，△AEF的周长为15，BC长为7，求△ABC的周长．

如图，BC⊥AE于点C，CD∥AB，∠1=55°，则∠B等于（    ）

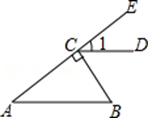
A．35°

B．45°

C．55°

D．65°

如图，直线a∥b，∠1=130°，则∠2=         ．