我们知道,顶点坐标为 的抛物线的解析式为 .今后我们还会学到,圆心坐标为 ,半径为 的圆的方程 ,如:圆心为 ,半径为3的圆的方程为 .
(1)以 为圆心, 为半径的圆的方程为 .
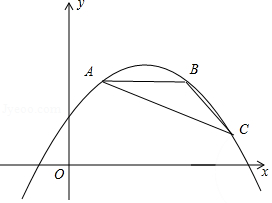
(2)如图,以 为圆心的圆与 轴相切于原点, 是 上一点,连接 ,作 ,垂足为 ,延长 交 轴于点 ,已知 .
①连接 ,证明: 是 的切线;
②在 上是否存在一点 ,使 ?若存在,求点 的坐标,并写出以 为圆心,以 为半径的 的方程;若不存在,请说明理由.

已知抛物线y=ax2+bx+c(0<2a<b)的顶点为P(x0,y0),点A(1,yA)、B(0,yB)、C(-1,yC)在该抛物线上.
(Ⅰ)当a=1,b=4,c=10时,①求顶点P的坐标;②求-的值;
(Ⅱ)当y0≥0恒成立时,求的最小值.
在平面直角坐标系中,抛物线 的顶点为 .
(1)求顶点 的坐标(用含有字母 的代数式表示);
(2)若点 , 在抛物线上,且 ,则 的取值范围是 ;(直接写出结果即可)
(3)当 时,函数 的最小值等于6,求 的值.
如图,在等腰直角三角形 中, ,点 在 轴上,点 在 轴上,点 ,二次函数 的图象经过点 .
(1)求二次函数的解析式,并把解析式化成 的形式;
(2)把 沿 轴正方向平移,当点 落在抛物线上时,求 扫过区域的面积;
(3)在抛物线上是否存在异于点 的点 ,使 是以 为直角边的等腰直角三角形?如果存在,请求出所有符合条件的点 的坐标;如果不存在,请说明理由.
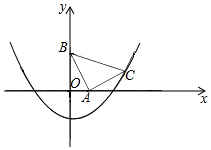
如图, 点 , , 都在抛物线 (其 中 上, 轴, ,且 .
(1) 填空: 抛物线的顶点坐标为 (用 含 的代数式表示) ;
(2) 求 的面积 (用 含 的代数式表示) ;
(3) 若 的面积为 2 ,当 时, 的最大值为 2 ,求 的值 .