对于二次函数 ,在下列几种说法中:①当 时. 随 的增大而减小;②若函数的图象与 轴有交点,则 ;③若 ,则二次函数 的图象在 轴的下方;④若将此函数的图象绕坐标
原点旋转 ,则旋转后的函数图象的顶点坐标为 ,其中正确的个数为
| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
如图,二次函数 的图象经过点 , ,下列说法正确的是

| A. |
|
B. |
|
| C. |
|
D. |
图象的对称轴是直线 |
二次函数 的图象如图所示,下列结论① ,② ,③ ,④ .其中正确的是
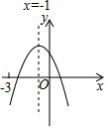
| A. |
①④ |
B. |
②④ |
C. |
②③ |
D. |
①②③④ |
二次函数 的图象如图所示,则直线 不经过的象限是

| A. |
第一象限 |
B. |
第二象限 |
C. |
第三象限 |
D. |
第四象限 |
小飞研究二次函数 为常数)性质时得到如下结论:
①这个函数图象的顶点始终在直线 上;
②存在一个 的值,使得函数图象的顶点与 轴的两个交点构成等腰直角三角形;
③点 , 与点 , 在函数图象上,若 , ,则 ;
④当 时, 随 的增大而增大,则 的取值范围为 .
其中错误结论的序号是
| A. |
① |
B. |
② |
C. |
③ |
D. |
④ |
已知 , 是非零实数, ,在同一平面直角坐标系中,二次函数 与一次函数 的大致图象不可能是
| A. |
|
| B. |
|
| C. |
|
| D. |
|
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:

①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0
其中正确结论的有( )
| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中错误的是( )

| A.a>0 |
| B.当x≥1时,y随x的增大而增大 |
| C.c<0 |
| D.当﹣1<x<3时,y>0 |
(年贵州省黔东南州)如图,已知二次函数 (
( )的图像如图所示,给出下列四个结论:①
)的图像如图所示,给出下列四个结论:① ;②
;② ;③
;③ ;④
;④ .其中正确的结论有( )
.其中正确的结论有( )

| A.1个 | B.2个 | C.3个 | D.4个 |
(年贵州省毕节)二次函数y=a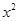 +bx+c的图象如图所示,则下列关系式错误的是( )
+bx+c的图象如图所示,则下列关系式错误的是( )
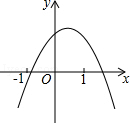
| A.a<0 | B.b>0 | C.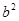 ﹣4ac>0 ﹣4ac>0 |
D.a+b+c<0 |
(年贵州省毕节)二次函数y=a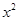 +bx+c的图象如图所示,则下列关系式错误的是( )
+bx+c的图象如图所示,则下列关系式错误的是( )
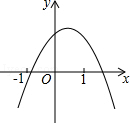
| A.a<0 | B.b>0 | C.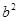 ﹣4ac>0 ﹣4ac>0 |
D.a+b+c<0 |
(2014年山东青岛3分)函数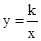 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A.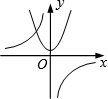 |
B. |
C.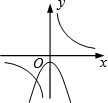 |
D.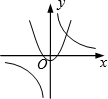 |