初中数学二次函数的性质解答题

定义：对于给定的两个函数，任取自变量的一个值，当时，它们对应的函数值互为相反数；当时，它们对应的函数值相等，我们称这样的两个函数互为相关函数．例如：一次函数，它的相关函数为．

（1）已知点在一次函数的相关函数的图象上，求的值；

（2）已知二次函数．①当点在这个函数的相关函数的图象上时，求的值；

②当时，求函数的相关函数的最大值和最小值；

（3）在平面直角坐标系中，点，的坐标分别为，，，，连结．直接写出线段与二次函数的相关函数的图象有两个公共点时的取值范围．

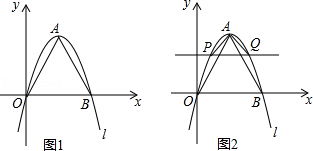
如图1，在平面直角坐标系中，点在轴正半轴上，的长度为，以为边向上作等边三角形，抛物线经过点，，三点

（1）当时，　　，当时，　　；

（2）根据（1）中的结果，猜想与的关系，并证明你的结论；

（3）如图2，在图1的基础上，作轴的平行线交抛物线于、两点，的长度为，当为等腰直角三角形时，和的关系式为　　；

（4）利用（2）（3）中的结论，求与的面积比．

如图1和图2，在中，，，．点在边上，点，分别在，上，且．点从点出发沿折线匀速移动，到达点时停止；而点在边上随移动，且始终保持．

（1）当点在上时，求点与点的最短距离；

（2）若点在上，且将的面积分成上下两部分时，求的长；

（3）设点移动的路程为，当及时，分别求点到直线的距离（用含的式子表示）；

（4）在点处设计并安装一扫描器，按定角扫描区域（含边界），扫描器随点从到再到共用时36秒．若，请直接写出点被扫描到的总时长．

如图，若是正数，直线与轴交于点；直线与轴交于点；抛物线的顶点为，且与轴右交点为．

（1）若，求的值，并求此时的对称轴与的交点坐标；

（2）当点在下方时，求点与距离的最大值；

（3）设，点，，，，，分别在，和上，且是，的平均数，求点，与点间的距离；

（4）在和所围成的封闭图形的边界上，把横、纵坐标都是整数的点称为“美点”，分别直接写出和时“美点”的个数．

设抛物线的解析式为 $y=a{x}^2$ ，过点 $B_1(1,0)$ 作 $x$ 轴的垂线，交抛物线于点 $A_1(1,2)$ ；过点 $B_2(\frac{1}{2}$ ， $0)$ 作 $x$ 轴的垂线，交抛物线于点 $A_2$ ； $\dots$ ；过点 $B_n({\left(\frac{1}{2}\right)}^{n-1}$ ， $0\left)\right(n$ 为正整数）作 $x$ 轴的垂线，交抛物线于点 $A_n$ ，连接 $A_n{B}_{n+1}$ ，得 $\mathit{Rt}$ △ $A_n{B}_n{B}_{n+1}$ ．

（1）求 $a$ 的值；

（2）直接写出线段 $A_n{B}_n$ ， $B_n{B}_{n+1}$ 的长（用含 $n$ 的式子表示）；

（3）在系列 $\mathit{Rt}$ △ $A_n{B}_n{B}_{n+1}$ 中，探究下列问题：

①当 $n$ 为何值时， $\mathit{Rt}$ △ $A_n{B}_n{B}_{n+1}$ 是等腰直角三角形？

②设 $1⩽k<m⩽n(k$ ， $m$ 均为正整数），问：是否存在 $\mathit{Rt}$ △ $A_k{B}_k{B}_{k+1}$ 与 $\mathit{Rt}$ △ $A_m{B}_m{B}_{m+1}$ 相似？若存在，求出其相似比；若不存在，说明理由．