有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数 与 的图象性质.
小明根据学习函数的经验,对函数 与 ,当 时的图象性质进行了探究.
下面是小明的探究过程:
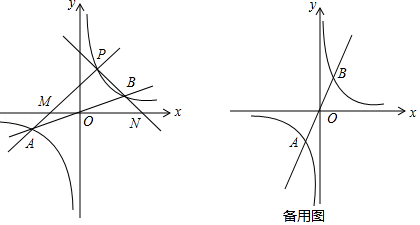
(1)如图所示,设函数 与 图象的交点为 , ,已知 点的坐标为 ,则 点的坐标为 ;
(2)若点 为第一象限内双曲线上不同于点 的任意一点.
①设直线 交 轴于点 ,直线 交 轴于点 .求证: .
证明过程如下:设 ,直线 的解析式为 .
则 ,
解得
直线 的解析式为
请你把上面的解答过程补充完整,并完成剩余的证明.
②当 点坐标为 , 时,判断 的形状,并用 表示出 的面积.
从数 ,1,2,5,8中任取一个数记作 ,则正比例函数 的图象经过第二、四象限的概率是 .
姜老师给出一个函数表达式,甲、乙、丙三位同学分别正确指出了这个函数的一个性质.甲:函数图象经过第一象限;乙:函数图象经过第三象限;丙:在每一个象限内, 值随 值的增大而减小.根据他们的描述,姜老师给出的这个函数表达式可能是
A. B. C. D.
如图,已知直线 ,双曲线 ,在 上取一点 , ,过 作 轴的垂线交双曲线于点 ,过 作 轴的垂线交 于点 ,过 作 轴的垂线交双曲线于点 ,过 作 轴的垂线交 于点 ,此时 与 重合,并得到一个正方形 ,若原点 在正方形 的对角线上且分这条对角线为 的两条线段,则 的值为 .
已知正比例函数 是常数, 的图象经过第二、四象限,那么 的值随着 的值增大而 .(填“增大”或“减小”
在平面直角坐标系中,点 , 在射线 上,点 , 在射线 上,以 为直角边作 ,以 为直角边作第二个 △ ,以 为直角边作第三个 △ , ,依此规律,得到 △ ,则点 的纵坐标为 .

在平面直角坐标系 中, 的直角顶点 在 轴上,点 的坐标为 ,将 沿直线 翻折,得到 △ ,过 作 垂直于 交 轴于点 ,则点 的坐标为

| A. |
|
B. |
|
C. |
|
D. |
|
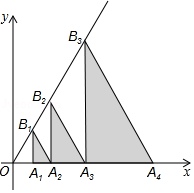
如图,过直线 上的点 作 ,交 轴于点 ,过点 作 轴.交直线 于点 ;过点 作 ,交 轴于点 ,过点 作 轴,交直线 于点 ; 按照此方法继续作下去,若 ,则线段 的长度为 .(结果用含正整数 的代数式表示)
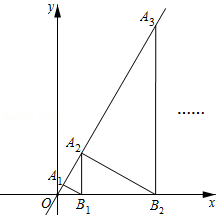
如图, 、 、 、… 都是等边三角形,其中 、 、… 都与x轴垂直,点A1、A2、…An都在x轴上,点B1、B2、…Bn都在直线 上,已知 ,则点A2016的坐标为 .
给出下列函数:① ;② ;③ ;④ ,上述函数中符合条件“当 时,函数值 随自变量 增大而增大“的是
A.①③B.③④C.②④D.②③