如图1,点 从 的顶点 出发,沿 匀速运动到点 ,图2是点 运动时,线段 的长度 随时间 变化的关系图象,其中 是曲线部分的最低点,则 的面积是
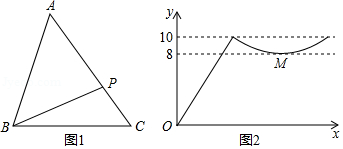
A.12B.24C.36D.48
如图1,在矩形 中,点 在 上, ,点 从点 出发,沿 的路径匀速运动到点 停止,作 于点 ,设点 运动的路程为 , 长为 ,若 与 之间的函数关系图象如图2所示,当 时, 的值是

A.2B. C. D.1
如图,平行四边形 中,对角线 、 相交于点 ,且 , , 是对角线 上任意一点,过点 作 ,与平行四边形的两条边分别交于点 、 .设 , ,则能大致表示 与 之间关系的图象为
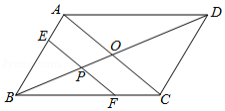
A.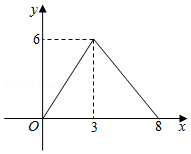
B.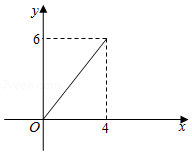
C.
D.
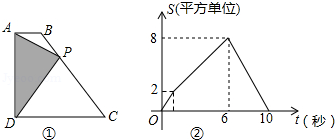
如图①,四边形 中, , , 从 点出发,以每秒1个单位长度的速度,按 的顺序在边上匀速运动,设 点的运动时间为 秒, 的面积为 , 关于 的函数图象如图②所示,当 运动到 中点时, 的面积为 .
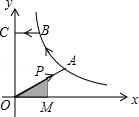
如图,已知A,B是反比例函数 图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿 (图中“→”所示路线)匀速运动,终点为C,过P作 轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
A.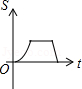 B.
B.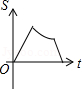
C.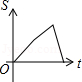 D.
D.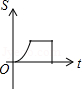
某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形 如图乙所示, 米, 米,在五边形 区域上种植花卉,则大正方形花坛种植花卉的面积 与 的函数图象大致是

A. B.
B.
C. D.
D.
如图,在正方形 中, ,动点 自 点出发沿 方向以每秒 的速度运动,同时动点 自 点出发沿折线 以每秒 的速度运动,到达 点时运动同时停止,设 的面积为 ,运动时间为 (秒 ,则下列图象中能大致反映 与 之间函数关系的是

A.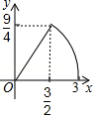 B.
B.
C. D.
D.
已知点 为某个封闭图形边界上一定点,动点 从点 出发,沿其边界顺时针匀速运动一周,设点 的运动时间为 ,线段 的长度为 ,表示 与 的函数图象大致如图所示,则该封闭图形可能是

A.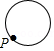 B.
B.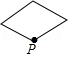 C.
C.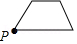 D.
D.
已知,等边三角形 和正方形 的边长相等,按如图所示的位置摆放 点与 点重合),点 、 、 共线, 沿 方向匀速运动,直到 点与 点重合.设运动时间为 ,运动过程中两图形重叠部分的面积为 ,则下面能大致反映 与 之间关系的函数图象是

A. B.
B.
C. D.
D.
如图,正方形 的对角线 , 相交于点 ,点 在 上由点 向点 运动(点 不与点 重合),连接 ,将线段 绕点 逆时针旋转 得到线段 ,连接 交 于点 .设 的长为 , 的长为 ,下列图象中大致反映 与 之间的函数关系的是

A. B.
B.
C. D.
D.
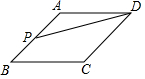
如图,点 P是菱形 ABCD边上的一动点,它从点 A出发沿在 A→ B→ C→ D路径匀速运动到点 D,设△ PAD的面积为 y, P点的运动时间为 x,则 y关于 x的函数图象大致为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
如图①,在边长为4cm的正方形ABCD中,点P以每秒2cm的速度从点A出发,沿AB→BC的路径运动,到点C停止.过点P作PQ∥BD,PQ与边AD(或边CD)交于点Q,PQ的长度y(cm)与点P的运动时间x(秒)的函数图象如图②所示.当点P运动2.5秒时,PQ的长是( )

A.2 cmB.3 cmC.4 cmD.5 cm
如图1,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度 (单位: 与运动时间 (单位: 的函数图象如图2,则该小球的运动路程 (单位: 与运动时间 (单位: 之间的函数图象大致是

A. B.
B.
C. D.
D.
如图,在等腰直角三角形 中, , , 是 边上的高,正方形 的边 在高 上, , 两点分别在 , 上.将正方形 以每秒 的速度沿射线 方向匀速运动,当点 与点 重合时停止运动.设运动时间为 ,正方形 与 重叠部分的面积为 ,则能反映 与 的函数关系的图象
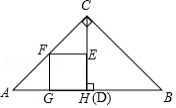
A.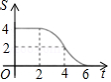 B.
B.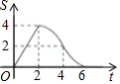
C.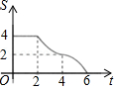 D.
D.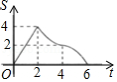
如图1,在 中, , , ,点D为AB的中点,线段 上有一动点E,连接DE,作DA关于直线DE的对称图形,得到 ,过点F作 于点G.设A、E两点间的距离为 , 两点间的距离为
小军根据学习函数的经验,对因变量y随自变量x的变化而变化的规律进行了探究.
下面是小军的探究过程,请补充完整.

(1)列表:如表的已知数据是根据A,E两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:
x/cm |
0 |
0.51 |
1.03 |
1.41 |
1.50 |
1.75 |
2.20 |
2.68 |
3.00 |
3.61 |
4.10 |
4.74 |
5.00 |
y/cm |
0 |
0.94 |
1.91 |
2.49 |
|
2.84 |
3.00 |
2.84 |
2.60 |
2.00 |
1.50 |
0.90 |
0.68 |
请你通过计算补全表格;
(2)描点、连线:在平面直角坐标系 中(如图2),描出表中各组数值所对应的点 ,并画出y关于x的图象;
(3)探究性质:随着x值的不断增大,y的值是怎样变化的? ;
(4)解决问题:当 时,FG的长度大约是 cm(保留两位小数).