初中数学平面直角坐标系填空题

平面直角坐标系中有两点M（a，b），N（c，d），规定（a，b）⊕（c，d）＝（a+c，b+d），则称点Q（a+c，b+d）为M，N的“和点”．若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形，则称这个四边形为“和点四边形”，现有点A（2，5），B（﹣1，3），若以O，A，B，C四点为顶点的四边形是“和点四边形”，则点C的坐标是　      ．

如图，等边三角形的顶点A（1，1）、B（3，1），规定把等边△ABC“先沿x轴翻折，再向左平移1个单位”为一次変换，如果这样连续经过2016次变换后，等边△ABC的顶点C的坐标为　　．

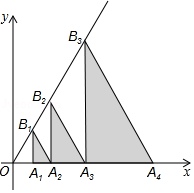
如图， $△O{B}_1{A}_2$、 $△O{B}_2{A}_3$、 $△O{B}_3{A}_4$、… $△O{B}_n{A}_n{}_{+1}$都是等边三角形，其中 $B_1{A}_1$、 $B_2{A}_2$、… $B_n{A}_n$都与x轴垂直，点A₁、A₂、…A_n都在x轴上，点B₁、B₂、…B_n都在直线 $y=\sqrt{3}x$上，已知 $O{A}_1＝1$，则点A₂₀₁₆的坐标为　　．

如图，在平面直角坐标系中，矩形 AOCB的两边 OA、 OC分别在 x轴和 y轴上，且 OA＝2， OC＝1．在第二象限内，将矩形 AOCB以原点 O为位似中心放大为原来的 $\frac{3}{2}$ 倍，得到矩形 A ₁ OC ₁ B ₁，再将矩形 A ₁ OC ₁ B ₁以原点 O为位似中心放大 $\frac{3}{2}$ 倍，得到矩形 A ₂ OC ₂ B ₂…，以此类推，得到的矩形 A _n O∁ _n B _n的对角线交点的坐标为 　　．

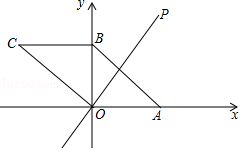
如图，在平面直角坐标系xOy中，▱ABCO的顶点A，B的坐标分别是A（3，0），B（0，2）．动点P在直线 $y=\frac{3}{2}x$上运动，以点P为圆心，PB长为半径的⊙P随点P运动，当⊙P与▱ABCO的边相切时，P点的坐标为　　．

如图，若菱形 ABCD的顶点 A， B的坐标分别为（3，0），（﹣2，0），点 D在 y轴上，则点 C的坐标是 　　．

如图，在平面直角坐标系中，已知 A（﹣1，0）， B（0，2），将△ ABO沿直线 AB翻折后得到△ ABC，若反比例函数 y＝ $\frac{k}{x}$ （ x＜0）的图象经过点 C，则 k＝ 　　．

在平面直角坐标系中，对于点 P（ a， b），我们把 Q（﹣ b+1， a+1）叫做点 P的伴随点，已知 A ₁的伴随点为 A ₂， A ₂的伴随点为 A ₃，…，这样依次下去得到 A ₁， A ₂， A ₃，…， A _n，若 A ₁的坐标为（3，1），则 A ₂₀₁₈的坐标为 　　．

若点 $M（k﹣1，k+1）$关于y轴的对称点在第四象限内，则一次函数 $y\mathit{＝（}k﹣1）x+k$的图象不经过第　　象限．

如图，直线l： $y=-\frac{4}{3}x$，点A₁坐标为（﹣3，0）．过点A₁作x轴的垂线交直线l于点B₁，以原点O为圆心，OB₁长为半径画弧交x轴负半轴于点A₂，再过点A₂作x轴的垂线交直线l于点B₂，以原点O为圆心，OB₂长为半径画弧交x轴负半轴于点A₃，…，按此做法进行下去，点A₂₀₁₆的坐标为　　．

如图，在平面直角坐标系中， $\Delta A_1{A}_2{A}_3，\Delta A_3{A}_4{A}_5，\Delta A_5{A}_6{A}_7，\Delta A_7{A}_8{A}_9，$…，都是等边三角形，且点A₁，A₃，A₅，A₇，A₉的坐标分别为 $A_1（3,0\mathit{），}{A}_3（1,0\mathit{），}{A}_5（4,0\mathit{），}{A}_7（0,0\mathit{），}{A}_9（5,0）$，依据图形所反映的规律，则A₁₀₀的坐标为　    　．

如图，以正六边形 ABCDEF的中心为坐标原点建立平面直角坐标系，顶点 C、 F在 x轴上，顶点 A的坐标为（1， ），则顶点 D的坐标为 　 　．

已知平行四边形 ABCD的顶点 A在第三象限，对角线 AC的中点在坐标原点，一边 AB与 x轴平行且 AB＝2，若点 A的坐标为（ a， b），则点 D的坐标为 　．

在平面直角坐标系中，点 P（ x， y）经过某种变换后得到点 P'（﹣ y+1， x+2），我们把点 P'（﹣ y+1， x+2）叫做点 P（ x， y）的终结点．已知点 P ₁的终结点为 P ₂，点 P ₂的终结点为 P ₃，点 P ₃的终结点为 P ₄，这样依次得到 P ₁、 P ₂、 P ₃、 P ₄、… P _n、…，若点 P ₁的坐标为（2，0），则点 P ₂₀₁₇的坐标为 　　．

如图，把矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在点A′的位置，若 $\mathit{OB}=\sqrt{5}$， $\text{tan}\angle \mathit{BOC}=\frac{1}{2}$,则点A′的坐标为　　．