初中数学根的判别式试题

如果关于 $x$的方程 $x^2-4x+m=0$有两个相等的实数根，那么 $m$的值是      .

已知关于 $x$的一元二次方程 $x^2-(m+1)x+\frac{1}{2}(m^2+1)=0$有实数根．

（1）求 $m$的值；

（2）先作 $y=x^2-(m+1)x+\frac{1}{2}(m^2+1)$的图象关于 $x$轴的对称图形，然后将所作图形向左平移3个单位长度，再向上平移2个单位长度，写出变化后图象的解析式；

（3）在（2）的条件下，当直线 $y=2x+n(n⩾m)$与变化后的图象有公共点时，求 $n^2-4n$的最大值和最小值．

已知关于 $x$的一元二次方程 $x^2+(k-5)x+1-k=0$，其中 $k$为常数．

（1）求证：无论 $k$为何值，方程总有两个不相等实数根；

（2）已知函数 $y=x^2+(k-5)x+1-k$的图象不经过第三象限，求 $k$的取值范围；

（3）若原方程的一个根大于3，另一个根小于3，求 $k$的最大整数值．

已知 $x_1$、 $x_2$是关于 $x$的方程 $x^2-\mathit{ax}-2=0$的两根，下列结论一定正确的是 $($　　 $)$

A． $x_1\ne x_2$B． $x_1+x_2>0$C． $x_1\cdot x_2>0$D． $x_1<0$， $x_2<0$

已知关于 $x$ 的一元二次方程 $x^2-\mathit{mnx}+m+n=0$ ，其中 $m$ ， $n$ 在数轴上的对应点如图所示，则这个方程的根的情况是 $($ 　　 $)$

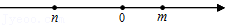
A．	有两个不相等的实数根	B．	有两个相等的实数根
C．	没有实数根	D．	无法确定

若关于 $x$的一元二次方程 $x^2-(2a+1)x+a^2=0$有两个不相等的实数根，求 $a$的取值范围．

关于 $x$的一元二次方程 $(m-1)x^2+2x-1=0$有两个不相等的实数根，则 $m$的取值范围是　    　．

关于 $x$的一元二次方程 $(a-1)x^2+(2a+1)x+a=0$有两个不相等的实数根，则 $a$的取值范围是　　．

若关于 $x$的方程 $x^2-2x+m=0$有两个相等的实数根，则实数 $m$的值等于　      　．

若关于 $x$的一元二次方程 $x^2-2x-k+1=0$有两个相等的实数根，则 $k$的值是 $($　　 $)$

A． $-1$B．0C．1D．2

一元二次方程 $4x^2-2x+\frac{1}{4}=0$的根的情况是 $($　　 $)$

A．有两个不相等的实数根B．有两个相等的实数根

C．没有实数根D．无法判断

关于 $x$的一元二次方程 $x^2+(k-3)x+1-k=0$根的情况，下列说法正确的是 $($　　 $)$

A．有两个不相等的实数根B．有两个相等的实数根

C．无实数根D．无法确定

关于 $x$的一元二次方程 $(a-1)x^2+2x+1=0$有两个实数根，则 $a$的取值范围为 $($　　 $)$

A． $a⩽2$   B． $a<2$   C． $a⩽2$且 $a\ne 1$   D． $a<2$且 $a\ne 1$

已知关于 $x$的一元二次方程 $x^2-(2k+1)x+k^2+k=0$．

（1）求证：无论 $k$取何值，方程都有两个不相等的实数根．

（2）如果方程的两个实数根为 $x_1$， $x_2$，且 $k$与 $\frac{x_1}{x_2}$都为整数，求 $k$所有可能的值．

关于 $x$的一元二次方程 $(m-1)x^2-2x-1=0$有两个实数根，则实数 $m$的取值范围是 $($　　 $)$

A． $m⩾0$B． $m>0$C． $m⩾0$且 $m\ne 1$D． $m>0$且 $m\ne 1$