初中数学一元二次方程选择题

若 $m$ 、 $n$ 是一元二次方程 $x^2+3x-9=0$ 的两个根，则 $m^2+4m+n$ 的值是 $($ 　　 $)$

A．

4

B．

5

C．

6

D．

12

已知关于 $x$ 的一元二次方程 $x^2-\mathit{mnx}+m+n=0$ ，其中 $m$ ， $n$ 在数轴上的对应点如图所示，则这个方程的根的情况是 $($ 　　 $)$

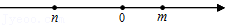
A．	有两个不相等的实数根	B．	有两个相等的实数根
C．	没有实数根	D．	无法确定

定义运算： $m$☆ $n=m{n}^2-\mathit{mn}-1$．例如：4☆ $2=4\times 2^2-4\times 2-1=7$．则方程1☆ $x=0$的根的情况为 $($　　 $)$

A．有两个不相等的实数根B．有两个相等的实数根

C．无实数根D．只有一个实数根

下列一元二次方程中，有两个不相等实数根的是 $($　　 $)$

A． $x^2-x+\frac{1}{4}=0$B． $x^2+2x+4=0$C． $x^2-x+2=0$D． $x^2-2x=0$

已知一元二次方程 $x^2+\mathit{kx}-3=0$有一个根为1，则 $k$的值为 $($　　 $)$

A． $-2$B．2C． $-4$D．4

已知 $x_1$、 $x_2$是关于 $x$的方程 $x^2-\mathit{ax}-2=0$的两根，下列结论一定正确的是 $($　　 $)$

A． $x_1\ne x_2$B． $x_1+x_2>0$C． $x_1\cdot x_2>0$D． $x_1<0$， $x_2<0$

已知关于 $x$ 的一元二次方程 $k{x}^2-(2k-1)x+k-2=0$ 有两个不相等的实数根，则实数 $k$ 的取值范围是 $($ 　　 $)$

A．

$k>-\frac{1}{4}$

B．

$k<\frac{1}{4}$

C．

$k>-\frac{1}{4}$ 且 $k\ne 0$

D．

$k<\frac{1}{4}$ 且 $k\ne 0$

若关于 $x$的一元二次方程 $x^2-2x-k+1=0$有两个相等的实数根，则 $k$的值是 $($　　 $)$

A． $-1$B．0C．1D．2

我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式．后人借助这种分割方法所得的图形证明了勾股定理，如图所示的矩形由两个这样的图形拼成，若 $a=3$， $b=4$，则该矩形的面积为 $($　　 $)$

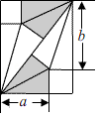
A．20B．24C． $\frac{99}{4}$D． $\frac{53}{2}$

欧几里得的《原本》记载，形如 $x^2+\mathit{ax}=b^2$的方程的图解法是：画 $\text{Rt}\Delta \text{ABC}$，使 $\angle \mathit{ACB}=90°$， $\mathit{BC}=\frac{a}{2}$， $\mathit{AC}=b$，再在斜边 $\mathit{AB}$上截取 $\mathit{BD}=\frac{a}{2}$．则该方程的一个正根是 $($　　 $)$

A． $\mathit{AC}$的长B． $\mathit{AD}$的长C． $\mathit{BC}$的长D． $\mathit{CD}$的长

我们知道方程 $x^2+2x-3=0$的解是 $x_1=1$， $x_2=-3$，现给出另一个方程 ${(2x+3)}^2+2(2x+3)-3=0$，它的解是 $($　　 $)$

A． $x_1=1$， $x_2=3$B． $x_1=1$， $x_2=-3$C． $x_1=-1$， $x_2=3$D． $x_1=-1$， $x_2=-3$

若直角三角形的两边长分别是方程 $x^2-7x+12=0$ 的两根，则该直角三角形的面积是 $($ 　　 $)$

A．

6

B．

12

C．

12或 $\frac{3\sqrt{7}}{2}$

D．

6或 $\frac{3\sqrt{7}}{2}$

方程 $x^2-x=56$ 的根是 $($ 　　 $)$

A．

$x_1=7$ ， $x_2=8$

B．

$x_1=7$ ， $x_2=-8$

C．

$x_1=-7$ ， $x_2=8$

D．

$x_1=-7$ ， $x_2=-8$

用配方法解方程 $x^2+2x-1=0$时，配方结果正确的是 $($　　 $)$

A． ${(x+2)}^2=2$B． ${(x+1)}^2=2$C． ${(x+2)}^2=3$D． ${(x+1)}^2=3$

某景点的参观人数逐年增加，据统计，2014年为10.8万人次，2016年为16.8万人次．设参观人次的平均年增长率为 $x$，则 $($　　 $)$

A． $10.8(1+x)=16.8$B． $16.8(1-x)=10.8$

C． $10.8{(1+x)}^2=16.8$D． $10.8\left[\right(1+x)+{(1+x)}^2]=16.8$