初中数学二元一次方程组试题

（年云南省曲靖市）某商场投入13800元资金购进甲、乙两种矿泉水共500箱，矿泉水的成本价和销售价如表所示：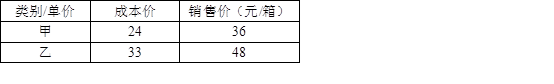

（1）该商场购进甲、乙两种矿泉水各多少箱？
（2）全部售完500箱矿泉水，该商场共获得利润多少元？

（年贵州省贵阳市）方程组的解为     ．

在“老年节”前夕，某公司工会组织323名退休职工到浙江杭州旅游，旅游前，工会确定每车保证有一名随团医生，并为此次旅游请了8名医生，现打算同时租甲、乙两种客车，其中甲种客车每辆载客50人，乙种客车每辆载客20人。
（1）请帮助工会设计租车方案。
（2）若甲种客车租金为800元/辆，乙种客车租金为600元/辆，工会按哪种方案租车最省钱？此时租金是多少？
（3）旅游前，一名医生由于有特殊情况，工会只能安排7名医生随团，为保证所租的每辆车安排有一名医生，租车方案调整为：同时租80座、50座和20座的大小三种客车，出发时，所租的三种客车的座位恰好坐满，请问工会的租车方案如何安排？

某学校为了绿化校园，决定从某苗圃购进甲、乙、丙三种树苗共80株，其中甲种树苗株树是乙种树苗株树的2倍，购买三种树苗的总金额不超过1320元，已知乙种树苗的单价是16元/株，乙种树苗的单价是甲种树苗的单价的，购买丙种树苗12株的金额等于购买甲种树苗20株的金额。
（1）甲、丙两种树苗的单价分别是多少元？
（2）若要求甲种树苗的株树不超过丙种树苗的株树，请你帮助设计共有哪些购买方案？

某校为了丰富学生的校园生活，准备购进一批价格分别为80元、60元的篮球和足球。该校打算用1000元购买篮球和足球，问恰好用完1000元，并且篮球、足球都买有的购买方案有哪几种？

假期到了，学校组织19名女教师去外地培训，住宿时有2人间和3人间可供安排，若每个房间都要住满，共有几种安排方案（ ）

A．5种

B．4种

C．3种

D．2种

盲盒为消费市场注入了活力，既能够营造消费者购物过程中的趣味体验，也为商家实现销售额提升拓展了途径．某商家将蓝牙耳机、多接口优盘、迷你音箱共22个，搭配为 $A$， $B$， $C$三种盲盒各一个，其中 $A$盒中有2个蓝牙耳机，3个多接口优盘，1个迷你音箱； $B$盒中蓝牙耳机与迷你音箱的数量之和等于多接口优盘的数量，蓝牙耳机与迷你音箱的数量之比为 $3:2$； $C$盒中有1个蓝牙耳机，3个多接口优盘，2个迷你音箱．经核算， $A$盒的成本为145元， $B$盒的成本为245元（每种盲盒的成本为该盒中蓝牙耳机、多接口优盘、迷你音箱的成本之和），则 $C$盒的成本为　　元．

如果一个自然数 $M$ 的个位数字不为0，且能分解成 $A\times B$ ，其中 $A$ 与 $B$ 都是两位数， $A$ 与 $B$ 的十位数字相同，个位数字之和为10，则称数 $M$ 为"合和数"，并把数 $M$ 分解成 $M=A\times B$ 的过程，称为"合分解"．

例如 $\because 609=21\times 29$ ，21和29的十位数字相同，个位数字之和为10，

$\therefore 609$ 是"合和数"．

又如 $\because 234=18\times 13$ ，18和13的十位数相同，但个位数字之和不等于10，

$\therefore 234$ 不是"合和数"．

（1）判断168，621是否是"合和数"？并说明理由；

（2）把一个四位"合和数" $M$ 进行"合分解"，即 $M=A\times B$ ． $A$ 的各个数位数字之和与 $B$ 的各个数位数字之和的和记为 $P\left(M\right)$ ； $A$ 的各个数位数字之和与 $B$ 的各个数位数字之和的差的绝对值记为 $Q\left(M\right)$ ．令 $G\left(M\right)=\frac{P\left(M\right)}{Q\left(M\right)}$ ，当 $G\left(M\right)$ 能被4整除时，求出所有满足条件的 $M$ ．

某公司生产的一种营养品信息如表．已知甲食材每千克的进价是乙食材的2倍，用80元购买的甲食材比用20元购买的乙食材多1千克．

营养品信息表
营养成份	每千克含铁42毫克
配料表	原料	每千克含铁
	甲食材	50毫克
	乙食材	10毫克
规格	每包食材含量	每包单价
$A$ 包装	1千克	45元
$B$ 包装	0.25千克	12元

（1）问甲、乙两种食材每千克进价分别是多少元？

（2）该公司每日用18000元购进甲、乙两种食材并恰好全部用完．

①问每日购进甲、乙两种食材各多少千克？

②已知每日其他费用为2000元，且生产的营养品当日全部售出．若 $A$ 的数量不低于 $B$ 的数量，则 $A$ 为多少包时，每日所获总利润最大？最大总利润为多少元？

某超市从厂家购进 $A$ 、 $B$ 两种型号的水杯，两次购进水杯的情况如表：

进货批次	$A$ 型水杯（个     $)$	$B$ 型水杯（个     $)$	总费用（元     $)$
一	100	200	8000
二	200	300	13000

（1）求 $A$ 、 $B$ 两种型号的水杯进价各是多少元？

（2）在销售过程中， $A$ 型水杯因为物美价廉而更受消费者喜欢．为了增大 $B$ 型水杯的销售量，超市决定对 $B$ 型水杯进行降价销售，当销售价为44元时，每天可以售出20个，每降价1元，每天将多售出5个，请问超市应将 $B$ 型水杯降价多少元时，每天售出 $B$ 型水杯的利润达到最大？最大利润是多少？

（3）第三次进货用10000元钱购进这两种水杯，如果每销售出一个 $A$ 型水杯可获利10元，售出一个 $B$ 型水杯可获利9元，超市决定每售出一个 $A$ 型水杯就为当地"新冠疫情防控"捐 $b$ 元用于购买防控物资．若 $A$ 、 $B$ 两种型号的水杯在全部售出的情况下，捐款后所得的利润始终不变，此时 $b$ 为多少？利润为多少？

“中国人的饭碗必须牢牢掌握在咱们自己手中”．为扩大粮食生产规模，某粮食生产基地计划投入一笔资金购进甲、乙两种农机具．已知购进2件甲种农机具和1件乙种农机具共需3.5万元，购进1件甲种农机具和3件乙种农机具共需3万元．

（1）求购进1件甲种农机具和1件乙种农机具各需多少万元？

（2）若该粮食生产基地计划购进甲、乙两农机具共10件，且投入资金不少于9.8万元又不超过12万元，设购进甲种农机具 $m$件，则有哪几种购买方案？哪种购买方案需要的资金最少，最少资金是多少？

（3）在（2）的方案下，由于国家对农业生产扶持力度加大，每件甲种农机具降价0.7万元，每件乙种农机具降价0.2万元，该粮食生产基地计划将节省的资金全部用于再次购买甲、乙两种农机具（可以只购买一种）请直接写出再次购买农机具的方案有哪几种？

为庆祝"中国共产党的百年华诞"，某校请广告公司为其制作"童心向党"文艺活动的展板、宣传册和横幅，其中制作宣传册的数量是展板数量的5倍，广告公司制作每件产品所需时间和利润如表：

产品	展板	宣传册	横幅
制作一件产品所需时间（小时）	1	$\frac{1}{5}$	$\frac{1}{2}$
制作一件产品所获利润（元 $)$	20	3	10

（1）若制作三种产品共计需要25小时，所获利润为450元，求制作展板、宣传册和横幅的数量；

（2）若广告公司所获利润为700元，且三种产品均有制作，求制作三种产品总量的最小值．