《九章算术》中有一道题的条件是:“今有大器五小器一容三斛,大器一小器五容二斛.”大致意思是:有大小两种盛米的桶,5大桶加1小桶共盛3斛米,1大桶加5小桶共盛2斛米,依据该条件,1大桶加1小桶共盛 斛米.(注斛是古代一种容量单位)
《九章算术》中记载:"今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?"其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数、羊价各是多少?设合伙人数为 人,羊价为 钱,根据题意,可列方程组为
| A. |
|
B. |
|
| C. |
|
D. |
|
四川省安岳县盛产柠檬和柚子两种水果,今年,某公司计划用两种型号的汽车运输柠檬和柚子到外地销售,运输中要求每辆汽车都要满载满运,且只能装运一种水果.若用3辆汽车装载柠檬、2辆汽车装载柚子可共装载33吨,若用2辆汽车装载柠檬、3辆汽车装载柚子可共装载32吨.
(1)求每辆汽车可装载柠檬或柚子各多少吨?
(2)据调查,全部销售完后,每吨柠檬可获利700元、每吨柚子可获利500元,计划用20辆汽车运输,且柚子不少于30吨,如何安排运输才能使公司获利最大,最大利润是多少元?
某服装专卖店计划购进,
两种型号的精品女装.已知2件
型女装和3件
型女装共需5600元;1件
型女装和2件
型女装共需3400元.
(1)求,
型女装的单价
(2)专卖店购进,
两种型号的女装共60件,其中
型的件数不少于
型件数的2倍,如果
型女装打八折,那么该专卖店至少需要准备多少贷款?
某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号中选择:
污水处理器型号 |
型 |
型 |
处理污水能力(吨 月) |
240 |
180 |
已知商家售出的2台 型、3台 型污水处理器的总价为44万元,售出的1台 型、4台 型污水处理器的总价为42万元.
(1)求每台 型、 型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?
为响应“把中国人的饭碗牢牢端在自己手中”的号召,确保粮食安全,优选品种,提高产量,某农业科技小组对 , 两个玉米品种进行实验种植对比研究.去年 、 两个品种各种植了10亩.收获后 、 两个品种的售价均为 元/kg,且 品种的平均亩产量比A品种高100千克, 、 两个品种全部售出后总收入为 元.
(1)求 、 两个品种去年平均亩产量分别是多少千克?
(2)今年,科技小组优化了玉米的种植方法,在保持去年种植面积不变的情况下,预计A、B两个品种平均亩产量将在去年的基础上分别增加 和 .由于B品种深受市场欢迎,预计每千克售价将在去年的基础上上涨 ,而A品种的售价保持不变, 、 两个品种全部售出后总收入将增加 .求a的值.
攀枝花芒果由于品质高、口感好而闻名全国,通过优质快捷的网络销售渠道,小明的妈妈先购买了2箱 品种芒果和3箱 品种芒果,共花费450元;后又购买了1箱 品种芒果和2箱 品种芒果,共花费275元(每次两种芒果的售价都不变).
(1)问 品种芒果和 品种芒果的售价分别是每箱多少元?
(2)现要购买两种芒果共18箱,要求 品种芒果的数量不少于 品种芒果数量的2倍,但不超过 品种芒果数量的4倍,请你设计购买方案,并写出所需费用最低的购买方案.
端午节前夕,某超市用1680元购进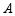 、
、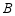 两种商品共60件,其中
两种商品共60件,其中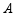 型商品每件24元,
型商品每件24元,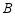 型商品每件36元.设购买
型商品每件36元.设购买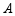 型商品
型商品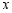 件、
件、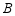 型商品
型商品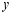 件,依题意列方程组正确的是
件,依题意列方程组正确的是
A.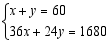 B.
B.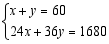
C.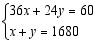 D.
D.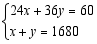
怡然美食店的 、 两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低 种菜品的售价,同时提高 种菜品的售价,售卖时发现, 种菜品售价每降0.5元可多卖1份; 种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?