已知代数式:①a2﹣2ab+b2;②(a﹣b)2.
(1)当a=5,b=3时,分别求代数式①和②的值;
(2)观察(1)中所求的两个代数式的值,探索代数式a2﹣2ab+b2和(a﹣b)2有何数量关系,并把探索的结果写出来;
(3)利用你探索出的规律,求128.52﹣2×128.5×28.5+28.52的值.
(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
① ② ③ ④
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示 ;
(3)利用(2)的结论计算9972+6×997+9的值.

已知a(a﹣1)﹣(a2﹣b)=﹣2,求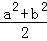 ﹣ab的值.
﹣ab的值.
图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状围成一个正方形.
(1)图②中的阴影部分是个______________形(填长方形或正方形),它的边长为;
(2)观察图②阴影部分的面积,请你写出三个代数式(m+n)2、(m-n)2、mn之间的等量关系是.
(3)实际上有许多代数恒等式可以用图形的面积来表示.如图③,它表示了.
如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方
形,然后按图②的方式拼成一个正方形。
(1)你认为图②中的阴影部分的正方形的边长等于_______________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积。
方法①______________.
方法②______________.
(3)观察图②,你能写出 ,
, ,mn这三个代数式间的等量关系吗?
,mn这三个代数式间的等量关系吗?
若x+y=3,且(x+2)(y+2)=12.
(1)求xy的值;
(2)求x2+3xy+y2的值.
比较 与 的大小.
(1)尝试(用“ ”,“ ”或“ ”填空)
①当 时, ;
②当 时, ;
③当 时, .
(2)归纳:若 取任意实数, 与 有怎样的大小关系?试说明理由.
图1是一个长为2 ,宽为2
,宽为2 的长方形,沿图中虚线剪开,可分成四块小长方形.
的长方形,沿图中虚线剪开,可分成四块小长方形.

(1)求出图1的长方形面积;
(2)将四块小长方形拼成一个图2的正方形.利用阴影部分面积的不同表示方法,直接写出代数式( )2、(
)2、( )2、
)2、 之间的等量关系;
之间的等量关系;
(3)把四块小长方形不重叠地放在一个长方形的内部(如图3),未被覆盖的部分用阴影表示.求两块阴影部分的周长和(用含 、
、 的代数式表示).
的代数式表示).
发现 任意五个连续整数的平方和是5的倍数.
验证 (1)的结果是5的几倍?
(2)设五个连续整数的中间一个为,写出它们的平方和,并说明是5的倍数.
延伸 任意三个连续整数的平方和被3除的余数是几呢?请写出理由.
请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:① 的值;②a﹣b的值.
的值;②a﹣b的值.