初中数学幂的乘方与积的乘方填空题

规定一种新的运算“*”：a*b＝，例如3*2＝＝10，那么*4＝______．

假设一家旅馆一共有30个房间，分别编以1-30号三十个号码，现在要在每个房间的钥匙上刻上数字，要求所刻数字必须使服务员很容易辨认是哪一个房间的钥匙，而使外人不容易猜到，现在有一种编码方法是：在每把钥匙上刻上两个数字，左边的一个数字是这把钥匙原来的房间号除以5所得的余数，而右边的一个数字是这把钥匙原来的房间号码除以7所得的余数，那么刻的数是36的钥匙所对应的原来房间应该是___________号．

已知f（x）=1+，其中f（a）表示当x＝a时代数式的值，如f（1）=1+，f（2）＝1＋，
f（a）=1+，则f（1）·f（2）·f（3）…·f（100）= ．

将一些相同的“○”按如图所示的规律依次摆放，观察每个“龟图”中的“○”的个数，则第10个“龟图”中的“○”的个数为 ．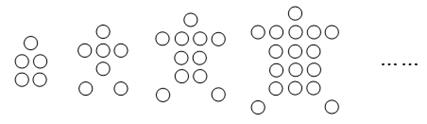

观察下列等式：
第1个等式：x₁=；
第2个等式：x₂=；
第3个等式：x₃=；
第4个等式：x₄=；
则x_l+x₂+x₃+…+x₁₀= ．

观察下图的变化规律，在第n个图中，三角形的个数为_______

将一刻度尺如图所示放在数轴上（数轴的单位长度是1cm），数轴上的两点A、B恰好与刻度尺上的“0cm”和“7cm”分别对应，若点A表示的数为﹣2.3，则点B表示的数应为 ．

如图，一只青蛙在圆周上标有数字的五个点上跳，若它停在奇数点上，则下一次沿顺时针方向跳两个点；若停在偶数点上，则下一次沿逆时针方向跳一个点，若青蛙从4这点开始跳，则经2015次跳后它停在数 对应的点上．

探索规律观察下面由※组成的图案和算式，解答问题

（1）请计算1+3+5+7+9+11=__________；
（2）请猜想1+3+5+7+9+…+19=__________；
（3）请猜想1+3+5+7+9+…+（2n﹣1）=__________；
（4）请用上述规律计算：21+23+25+…+99．

如果+=0，那么，

，则为．

（本题8分）小明有5张写着不同数字的卡片，请你按要求抽出卡片，完成下列各问题：

（1）从中取出2张卡片，使这2张卡片上数字的乘积最小，乘积的最小值为 ；
（2）从中取出4张卡片，用学过的运算方法，使结果为24。写出运算式子。
（写出一种即可）算24的式子为 。

（本题12分）意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和．现以这组数中的各个数作为正方形的边长值构造正方形：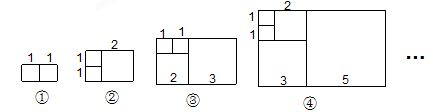

再分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、③、④、 …相应长方形的周长如下表所示：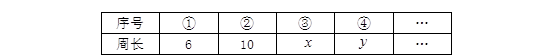

仔细观察图形，上表中的x= ，y= ．
若按此规律继续作长方形，则序号为⑧的长方形周长是 ．

如图，在数轴上A点表示数﹣2，B点表示数6，若在原点O处放一挡板，一小球甲从点A处以1个单位/秒的速度向左运动；同时另一小球乙从点B处以2个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，则经过 秒，甲、乙两小球到原点的距离相等．

设[x）表示大于x的最小整数，如[3）＝4，[－1．2）＝－1，则下列结论中正确的是_______．（填写所有正确结论的序号）①[0）＝0；②[x）－x的最小值是0；③[x）－x的最大值是0；④存在实数x，使[x）－x＝0．5成立。