初中数学规律型：图形的变化类试题

观察下列图形：它们是按一定规律排列的，依照此规律，第9个图形中共有　　个点．

图①是一块边长为1，周长记为的正三角形（三边相等的三角形）纸板，沿图①的底边剪去一块边长为的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪掉正三角形纸板边长的）后，得图③，④，…，记第n（n3）块纸板的周长为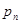，则的值为（  ）

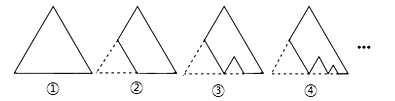
A．

B．

C．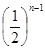

D．

电子跳蚤游戏盘是如图所示的△ABC，AB=6，AC=7，BC=8．如果跳蚤开始时在BC边的P₀处，BP₀=2．跳蚤第一步从P₀跳到AC边的P₁（第1次落点）处，且CP₁=CP₀；第二步从P₁跳到AB边的P₂（第2次落点）处，且AP₂=AP₁；第三步从P₂跳到BC边的P₃（第3次落点）处，且BP₃=BP₂；…；跳蚤按上述规则一直跳下去，第n次落点为P_n（n为正整数），则点P₂₀₀₇与P₂₀₁₀之间的距离为（ ）

A．1

B．2

C．3

D．4

观察下列图形的排列规律（其中、■、★分别表示三角形、正方形、五角星）．若第一个图形是三角形，则第18个图形是           ．（填图形的名称）
■★■★■★■★…

“分块计数法”：对有规律的图形进行计数时，有些题可以采用“分块计数”的方法．

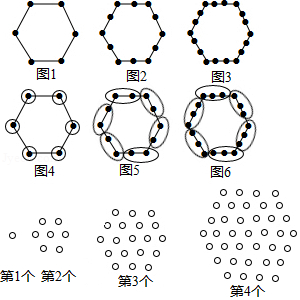
例如：图1有6个点，图2有12个点，图3有18个点， $\dots \dots$，按此规律，求图10、图 $n$有多少个点？

我们将每个图形分成完全相同的6块，每块黑点的个数相同（如图），这样图1中黑点个数是 $6\times 1=6$个；图2中黑点个数是 $6\times 2=12$个：图3中黑点个数是 $6\times 3=18$个； $\dots \dots$；所以容易求出图10、图 $n$中黑点的个数分别是　　、　　．

请你参考以上“分块计数法”，先将下面的点阵进行分块，再完成以下问题：

（1）第5个点阵中有　　个圆圈；第 $n$个点阵中有　　个圆圈．

（2）小圆圈的个数会等于271吗？如果会，请求出是第几个点阵．

观察下列图形，则第个图形中三角形的个数是________

如图，在 $\mathit{\Delta ABC}$中， $\mathit{AB}=5$， $\mathit{AC}=4$，若进行以下操作，在边 $\mathit{BC}$上从左到右依次取点 $D_1$、 $D_2$、 $D_3$、 $D_4$、 $\dots$；过点 $D_1$作 $\mathit{AB}$、 $\mathit{AC}$的平行线分别交 $\mathit{AC}$、 $\mathit{AB}$于点 $E_1$、 $F_1$；过点 $D_2$作 $\mathit{AB}$、 $\mathit{AC}$的平行线分别交 $\mathit{AC}$、 $\mathit{AB}$于点 $E_2$、 $F_2$；过点 $D_3$作 $\mathit{AB}$、 $\mathit{AC}$的平行线分别交 $\mathit{AC}$、 $\mathit{AB}$于点 $E_3$、 $F_3\dots$，则 $4(D_1{E}_1+D_2{E}_2+\dots +D_{2019}{E}_{2019})+5(D_1{F}_1+D_2{F}_2+\dots +D_{2019}{F}_{2019})=$　        　．

图1是由若干个小圆圈堆成的一个形如等边三角形的图案，最上面一层有一个圆圈，
以下各层均比上一层多一个圆圈，一共堆了n 层．将图1倒置后与原图1拼成图2的形状，这样我们可以
算出图1中所有圆圈的个数为1＋2＋3＋…＋n＝．

如果图中的圆圈共有13层，请解决下列问题：
（1）我们自上往下，在每个圆圈中按图3的方式填上一串连续的正整数1，2，3，4，……，则最底层最左
边这个圆圈中的数是         ；
（2）我们自上往下，在每个圆圈中按图4的方式填上一串连续的整数－23，－22，－21，－20，……，求
最底层最右边圆圈内的数是_______；
（3）求图4中所有圆圈中各数的绝对值之和．

一质点P从距原点1个单位的M点处向原点方向跳动，第一次跳动到OM的中点M₁处，第二次从M₁跳到OM₁的中点M₂处，第三次从点M₂跳到OM₂的中点M₃处，如此不断跳动下去，则第n次跳动后，该质点到原点O的距离为（   ）

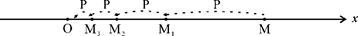
A．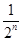

B．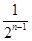

C．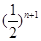

D．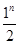

下面图形都是由同样大小的小球按一定规律排列的，依照此规律排列下去，第   

　　个图形共有210个小球．

如图，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第20个图需要黑色棋子的个数为　 　．

下列图形都是由同样大小的实心圆点按一定规律组成的，其中第①个图形一共有5个实心圆点，第②个图形一共有8个实心圆点，第③个图形一共有11个实心圆点，…，按此规律排列下去，第⑥个图形中实心圆点的个数为（　　）

A．

$18$

B．

$19$

C．

$20$

D．

$21$

下列图案是用长度相同的火柴棒按一定规律拼搭而成，图案①需8根火柴棒，图案②需15根火柴棒， $\dots$，按此规律，图案⑦需　　根火柴棒．

将一些相同的“〇”按如图所示摆放，观察每个图形中的“〇”的个数，若第 $n$个图形中“〇”的个数是78，则 $n$的值是 $($　　 $)$

A．11B．12C．13D．14

如图图形都是由同样大小的菱形按照一定规律所组成的，其中第①个图形中一共有3个菱形，第②个图形中一共有7个菱形，第③个图形中一共有13个菱形，，按此规律排列下去，第⑦个图形中菱形的个数为　 　．