初中数学规律型：数字的变化类解答题

观察下列等式，探究其中的规律：




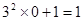
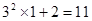
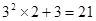
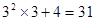
（1）根据以上观察，计算：①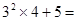             
②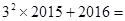                
（2）猜想：当n为自然数时，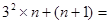              

如图，平面内有公共端点的6条射线O

A．O

B．O

C．O

D．OE、OF，按照图中的规律，从射线OA开始，按照逆时针方向，依次在射线上画点表示1，2，3，4，5，6，7，…

（1）根据图中规律，表示“19”的点在射线          上；
（2）按照图中规律推算，表示“2014”的点在射线          上；
（3）请你写出在射线OC上表示的数的规律（用含的代数式表示）                   ．

寻找公式，求代数式的值：从2开始，连续的偶数相加，它们的和的情况如下表：

（1）当n个最小的连续正偶数相加时，它们的和S与n之间的关系，用公式表示为_________________；
（2）并按此规律计算： ①2+4+6+…+300的值；  ②162+164+166+…+400的值．

某城市大剧院地面的一部分为扇形，观众席的座位按下列方式设置：

排数	1	2	3	4
座位数	50	53	56	59

 
按这种方式排下去，
（1）第5、6排各有多少个座位？
（2）第n排有多少个座位？
（3）根据（2）的代数式，判断第25排有多少个座位？

观察下列一组等式的化简．然后解答后面的 问题：
；
；
…
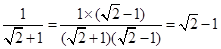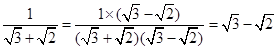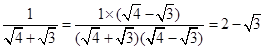（1）在计算结果中找出规律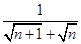=      （n表示大于0的自然数）
（2）通过上述化简过程，可知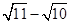      （填“＞”、“＜”或“=”）；
（3）利用你发现的规律计算下列式子的值：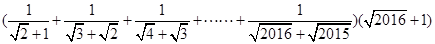

观察：从2开始，连续的偶数相加，它们的和的情况如下图：

（1）当加数m的个数为n时，和（S）与n之间有什么样的数量关系，用公式表示出来；
（2）按此规律计算（写出必要的演算过程）：
①2＋4＋6＋…＋300的值；
②162＋164＋166＋…＋400的值．

观察下面的变形规律：
 ＝1－；＝－；＝－；……解答下面的问题：
（1）若n为正整数，请你猜想＝                   ；
（2）求和：＋＋．（注：只能用上述结论做才能给分）；
（3）用上述相似的方法求和：．

（本题6分）先看数列：1，2，4，8，…，2⁶³．从第二项起，每一项与它的前一项的比都等于2，象这样，一个数列：a₁，a₂，a₃，…，a_n﹣1，a_n；从它的第二项起，每一项与它的前一项的比都等于一个常数q，那么这个数列就叫等比数列，q叫做等比数列的公比．
根据你的阅读，回答下列问题：
（1）请你写出一个等比数列，并说明公比是多少？
（2）请你判断下列数列是否是等比数列，并说明理由；，，，，…；
（3）有一个等比数列a₁，a₂，a₃，…，a_n﹣1，a_n；已知a₁=5，q=﹣3；请求出它的第25项a₂₅．（结果不需化简,可以保留乘方的形式）