如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如 ,表示
,则
的最小值为
,表示
,则
的最小值为

A.32B.36C.38D.40
如图,正方形 的边长为2,其面积标记为 ,以 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为 , ,按照此规律继续下去,则 的值为

A. B. C. D.
定义一种对正整数 的“ ”运算:①当 为奇数时, ;②当 为偶数时, (其中 是使 为奇数的正整数) ,两种运算交替重复进行,例如,取 ,则:

若 ,则第2018次“ ”运算的结果是
A.1B.4C.2018D.
我国南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项式 的展开式的各项系数,此三角形称为“杨辉三角”

根据”杨辉三角”请计算 的展开式中从左起第四项的系数为
A.84B.56C.35D.28
观察下面“品”字形中各数之间的规律,根据观察到的规律得出 的值为

A.23B.75C.77D.139
在一列数: , , , , 中, , ,从第三个数开始,每一个数都等于它前两个数之积的个位数字,则这一列数中的第2017个数是
A.1B.3C.7D.9
如表是一个 行 4 列共 16 个“数” 组成) 的奇妙方阵, 从这个方阵中选四个“数”, 而且这四个“数”中的任何两个不在同一行, 也不在同一列, 有很多选法, 把每次选出的四个“数”相加, 其和是定值, 则方阵中第三行三列的“数”是
|
|
|
|
|
|
|
0 |
|
6 |
|
|
|
4 |
|
|
A . 5B . 6C . 7D . 8
观察下列关于自然数的式子:
①
②
③
根据上述规律,则第2017个式子的值是
A.8064B.8065C.8066D.8067
我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项式 的展开式的各项系数,此三角形称为“杨辉三角”.
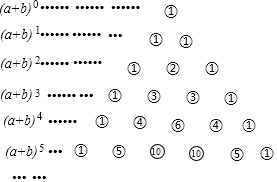
根据“杨辉三角”请计算 的展开式中第三项的系数为
A.2017B.2016C.191D.190
按一定规律排列的一列数依次为:2,3,10,15,26,35, ,按此规律排列下去,则这列数中的第100个数是
A.9999B.10000C.10001D.10002
将一组数 ,2, , , , , ,按下列方式进行排列:
,2, , , ;
, ,4, , ;
若2的位置记为 , 的位置记为 ,则 这个数的位置记为
A. B. C. D.
观察以下一列数的特点:0,1, ,9, ,25, ,则第11个数是
A. B. C.100D.121