观察下列等式:
第一个等式: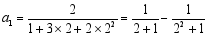
第二个等式: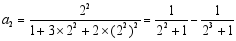
第三个等式: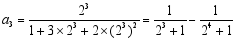
第四个等式: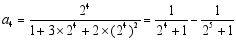
按上述规律,回答下列问题:
(1)请写出第六个等式: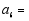
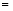 ;
;
(2)用含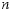 的代数式表示第
的代数式表示第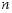 个等式:
个等式: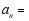
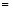 ;
;
(3)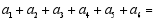 (得出最简结果);
(得出最简结果);
(4)计算: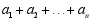 .
.
我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将 化为分数形式
由于 ,设 ①
则 ②
② ①得 ,解得 ,于是得 .
同理可得 ,
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(基础训练)
(1) , ;
(2)将 化为分数形式,写出推导过程;
(能力提升)
(3) , ;
(注 ,
(探索发现)
(4)①试比较 与1的大小: 1(填“ ”、“ ”或“ ”
②若已知 ,则 .
(注
有一列按一定顺序和规律排列的数:
第一个数是 ;
第二个数是 ;
第三个数是 ;
对任何正整数 ,第 个数与第 个数的和等于 .
(1)经过探究,我们发现: , , ,
设这列数的第5个数为 ,那么 , , ,哪个正确?
请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第 个数(即用正整数 表示第 数),并且证明你的猜想满足"第 个数与第 个数的和等于 ";
(3)设 表示 , , , , ,这2016个数的和,即 ,
求证: .
将连续的偶数2,4,6,8,10……排成如下的数表.
(1)十字框的五个数的和与中间的数26有什么关系?
(2)设中间的数为m,用代数式表示十字框中的五个数之和;
(3)十字框中的五个数之和能等于2 060吗?若能,请写出这五个数;若不能,请说明理由.