有一列按一定顺序和规律排列的数:
第一个数是 ;
第二个数是 ;
第三个数是 ;
对任何正整数 ,第 个数与第 个数的和等于 .
(1)经过探究,我们发现: , , ,
设这列数的第5个数为 ,那么 , , ,哪个正确?
请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第 个数(即用正整数 表示第 数),并且证明你的猜想满足"第 个数与第 个数的和等于 ";
(3)设 表示 , , , , ,这2016个数的和,即 ,
求证: .
相关知识点
推荐套卷
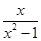 (
(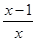 -2),其中x=2.
-2),其中x=2.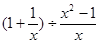
 ,其中x=-2.
,其中x=-2. ,其中x是一元二次方程
,其中x是一元二次方程 的正数根.
的正数根.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号