观察下列两行数:
1,3,5,7,9,11,13,15,17,
1,4,7,10,13,16,19,22,25,
探究发现:第1个相同的数是1,第2个相同的数是7, ,若第 个相同的数是103,则 等于
A.18B.19C.20D.21
填在下面各正方形中四个数之间都有相同的规律,根据这种规律 的值为

A.180B.182C.184D.186
将从1开始的连续奇数按如图所示的规律排列,例如,位于第4行第3列的数为27,则位于第32行第13列的数是

| A. |
2025 |
B. |
2023 |
C. |
2021 |
D. |
2019 |
将正整数1至2018按一定规律排列如下表:
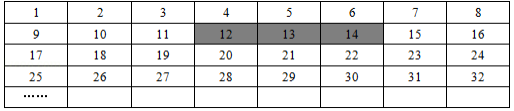
平移表中带阴影的方框,方框中三个数的和可能是
A.2019B.2018C.2016D.2013
根据图中数字的规律,若第 个图中的 ,则 的值为

| A. |
100 |
B. |
121 |
C. |
144 |
D. |
169 |
将全体正奇数排成一个三角形数阵:
1
3 5
7 9 11
13 15 17 19
21 23 25 27 29
按照以上排列的规律,第25行第20个数是
A.639B.637C.635D.633
生活中常用的十进制是用 这十个数字来表示数,满十进一,例: , ;计算机也常用十六进制来表示字符代码,它是用 来表示 ,满十六进一,它与十进制对应的数如表:
| 十进制 |
0 |
1 |
2 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
| 十六进制 |
0 |
1 |
2 |
|
8 |
9 |
|
|
|
|
|
|
10 |
11 |
|
例:十六进制 对应十进制的数为 , 对应十进制的数为 ,那么十六进制中 对应十进制的数为
| A. |
28 |
B. |
62 |
C. |
238 |
D. |
334 |
1261年,我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律,比欧洲的相同发现要早三百多年,我们把这个三角形称为“杨辉三角”,请观察图中的数字排列规律,则 , , 的值分别为

A. , , B. , ,
C. , , D. , ,
已知 为实数,规定运算: , , , , , .按上述方法计算:当 时, 的值等于
| A. |
|
B. |
|
C. |
|
D. |
|
如图,是按一定规律排成的三角形数阵,按图中数阵的排列规律,第9行从左至右第5个数是
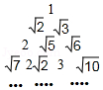
A. B. C. D.
按规律排列的一组数据: , ,□, , , , ,其中□内应填的数是
| A. |
|
B. |
|
C. |
|
D. |
|