观察下列一组数的排列规律:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
那么,这一组数的第2019个数是 .
从 ,1,2,4四个数中任取两个不同的数(记作 , 构成一个数组 , (其中 , ,且将 , 与 , 视为同一个数组),若满足:对于任意的 , 和 , , , 都有 ,则 的最大值
| A. |
10 |
B. |
6 |
C. |
5 |
D. |
4 |
阅读下面的材料:
按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为,排在第二位的数称为第二项,记为
,依此类推,排在第
位的数称为第
项,记为
.所以,数列的一般形式可以写成:
,
,
,
,
,
.
一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,公差通常用表示.如:数列1,3,5,7,
为等差数列,其中
,
,公差为
.
根据以上材料,解答下列问题:
(1)等差数列5,10,15,的公差
为 ,第5项是 .
(2)如果一个数列,
,
,
,
,是等差数列,且公差为
,那么根据定义可得到:
,
,
,
,
,
.
所以
,
,
由此,请你填空完成等差数列的通项公式:
.
(3)是不是等差数列
,
,
的项?如果是,是第几项?
我们知道,很多数学知识相互之间都是有联系的.如图,图一是“杨辉三角”数阵,其规律是:从第三行起,每行两端的数都是“1”,其余各数都等于该数“两肩”上的数之和;图二是二项和的乘方(a+b)n的展开式(按b的升幂排列).经观察:图二中某个二项和的乘方的展开式中,各项的系数与图一中某行的数一一对应,且这种关系可一直对应下去.将(s+x)15的展开式按x的升幂排列得:(s+x)15=a0+a1x+a2x2+…+a15x15.
依上述规律,解决下列问题:
(1)若s=1,则a2= ;
(2)若s=2,则a0+a1+a2+…+a15= .

探索与发现:下面是用分数(数字表示面积)砌成的“分数墙”,则整面“分数墙”的总面积是 .

如图,在以为直角顶点的等腰直角三角形纸片
中,将
角折起,使点
落在
边上的点
(不与点
,
重合)处,折痕是
.

如图1,当时,
;
如图2,当时,
;
如图3,当时,
;
依此类推,当为正整数)时,
.
南宋数学家杨辉在其著作《详解九章算法》中揭示了 为非负整数)展开式的项数及各项系数的有关规律如下,后人也将右表称为"杨辉三角"
则 展开式中所有项的系数和是

| A. |
128 |
B. |
256 |
C. |
512 |
D. |
1024 |
数轴上,
两点的距离为4,一动点
从点
出发,按以下规律跳动:第1次跳动到
的中点
处,第2次从
点跳动到
的中点
处,第3次从
点跳动到
的中点
处,按照这样的规律继续跳动到点
,
,
,
,
.
,
是整数)处,那么线段
的长度为 .

已知有理数 ,我们把 称为 的差倒数,如:2的差倒数是 , 的差倒数是 .如果 , 是 的差倒数, 是 的差倒数, 是 的差倒数 依此类推,那么 的值是
| A. |
|
B. |
7.5 |
C. |
5.5 |
D. |
|
观察下列一组数:
,
,
,
,
,
,
它们是按一定规律排列的,请利用其中规律,写出第个数
(用含
的式子表示)
阅读下列材料:小明为了计算的值,采用以下方法:
设①
则②
②①得
请仿照小明的方法解决以下问题:
(1)
;
(2) ;
(3)求的和
,
是正整数,请写出计算过程).
如图,过点 作 轴的垂线交直线 于点 ,过点 作直线 的垂线,交 轴于点 ,过点 作 轴的垂线交直线 于点 , ,这样依次下去,得到△ ,△ ,△ , ,其面积分别记为 , , , ,则 为
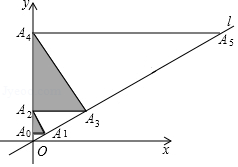
| A. |
|
B. |
|
C. |
|
D. |
|