初中数学代数式求值解答题

某自行车厂计划每天平均生产n辆自行车，而实际产量与计划产量相比有出入．下表记录了某周五个工作日每天实际产量情况（超过计划产量记为正、少于计划产量记为负）：

星期	一	二	三	四]	五
实际生产量	+5	﹣2	﹣4	+13	﹣3

 
（1）用含n的代数式表示本周前三天生产自行车的总数；
（2）该厂实行每日计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，当n=100时，那么该厂工人这一周的工资总额是多少元？
（3）若将上面第（2）问中“实行每日计件工资制”改为“实行每周计件工资制”，其他条件不变，当n=100时，在此方式下这一周工人的工资与按日计件的工资哪一个更多？请说明理由．

已知b、c互为相反数，m、n互为倒数，x的绝对值为2．求代数式的值．

重百商场正销售某品牌的一款等离子宽屏幕电视机，年初时售价定为元，3月份售价降低了元．由于伦敦奥运会的举行，8月份销售看好，故商场决定将售价在3月份的基础上上涨10%．奥运会结束后，由于销售不畅，故商场决定将售价在8月份的基础上下调10%．
（1）请用代数式表示该款等离子宽屏幕电视机现在的价格；
（2）若年初时售价定为6500元，3月初售价降低了500元，那么该款等离子宽屏幕电视机现在的价格是多少元？

某城市出租车收费标准如下：3公里以内（含3公里）收费8元，超过3公里的部分每公里收费1.5元．
（1）若行驶x公里（x为整数），试用含x的代数式表示应收的车费；
（2）若某人乘坐出租汽车行驶8公里，则应付车费多少元？

如图，将边长为 $m$的正方形纸板沿虚线剪成两个小正方形和两个矩形，拿掉边长为 $n$的小正方形纸板后，将剩下的三块拼成新的矩形．

（1）用含 $m$或 $n$的代数式表示拼成矩形的周长；

（2） $m=7$， $n=4$，求拼成矩形的面积．

若、互为相反数，、互为倒数，的绝对值等于2，计算的值。

“囧”（jiǒng）曾经是一个风靡网络的流行词，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．

（1）用含有x、y的代数式表示右图中“囧”（阴影部分）的面积；
（2）当x＝2y＝8时，求此时“囧”的面积；

观察：从2开始，连续的偶数相加，它们的和的情况如下图：

（1）当加数m的个数为n时，和（S）与n之间有什么样的数量关系，用公式表示出来；
（2）按此规律计算（写出必要的演算过程）：
①2＋4＋6＋…＋300的值；
②162＋164＋166＋…＋400的值．

某居民统计了家里的用水量x（立方米）与应缴水费w（元）之间的关系如下表所示．

（1）写出用水量x（立方米）与水费w（元）之间的关系式．
（2）计算用水量是35立方米时的水费是多少元？

（1）当时，求代数式的值．
（2）已知的值为7 , 求代数式的值

比较 $x^2+1$与 $2x$的大小．

（1）尝试（用“ $<$”，“ $=$”或“ $>$”填空） $:$

①当 $x=1$时， $x^2+1$　　 $2x$；

②当 $x=0$时， $x^2+1$　　 $2x$；

③当 $x=-2$时， $x^2+1$　　 $2x$．

（2）归纳：若 $x$取任意实数， $x^2+1$与 $2x$有怎样的大小关系？试说明理由．

某城市为了鼓励居民节约用水，对自来水用户按如下标准收费：若每月每户用水的最高标准为10吨，超过标准的部分加价收费，不超过10吨，每吨按2.9元收费，超过10吨的部分按每吨4元收费，
（1）某用户3月份用水x吨，请用含x的代数式表示应交水费
（2）求当x=25时的水费．

已知长方形的长为（3a+4b），宽比长短（b─a），设长方形的周长为C．
（1）用含a，b的代数式表示C；
（2）若，求C的值．

某餐厅中，一张桌子可坐6人，有以下两种摆放方式：
（1）当有张桌子时，两种摆放方式各能坐多少人？
（2）一天中午餐厅要接待98位顾客共同就餐，但餐厅只有25张这样的餐桌，若你是这个餐厅的经理，你打算选择哪种方式来摆放餐桌，为什么？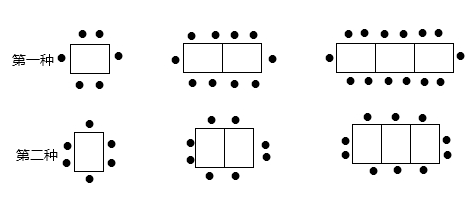

某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元．厂方在开展促销活动期间，向客户提供两种优惠方案：
①买一套西装送一条领带；
②西装和领带都按定价的90%付款．
现某客户要到该服装厂购买西装20套，领带x条（x＞20）．
（1）若该客户按方案①购买，需付款                        元（用含x的代数式表示）；
若该客户按方案②购买，需付款                        元（用含x的代数式表示）；
（2）若x=30，通过计算说明此时按哪种方案购买较为合算？