如图，将边长为 的正方形纸板沿虚线剪成两个小正方形和两个矩形，拿掉边长为 的小正方形纸板后，将剩下的三块拼成新的矩形．
（1）用含 或 的代数式表示拼成矩形的周长；
（2） ， ，求拼成矩形的面积．
“囧”（jiǒng）曾经是一个风靡网络的流行词，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．
（1）用含有x、y的代数式表示右图中“囧”（阴影部分）的面积；
（2）当x＝2y＝8时，求此时“囧”的面积；
某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元．厂方在开展促销活动期间，向客户提供两种优惠方案：①西装和领带都按定价的90%付款；②买一套西装送一条领带．现某客户要到该服装厂购买x套西装（x≥1），领带条数是西装套数的4倍多5．
（1）若该客户按方案①购买，需付款 元：（用含x的代数式表示）
若该客户按方案②购买，需付款 元；（用含x的代数式表示）
（2）若x=10，通过计算说明此时按哪种方案购买较为合算？
眉山市三苏雕像广场是为了纪念三苏父子而修建的．原是一块长为
米，宽为
米的长方形地块，现在政府对广场进行改造，计划将如图四周阴影部分进行绿化，中间将保留边长为
米的正方形三苏父子雕像，则绿化的面积是多少平方米？并求出当
时的绿化面积．
某单位在五月份准备组织部分员工到北京旅游，现联系了甲、乙两家旅行社，两家旅行社报价均为2000元/人，两家旅行社同时都对10人以上的团体推出了优惠举措：甲旅行社对每位员工七五折优惠；而乙旅行社是免去一位带队管理员工的费用，其余员工八折优惠．
（1）如果设参加旅游的员工共有a（a＞10）人，则甲旅行社的费用为 元，乙旅行社的费用为 元；（用含a的代数式表示，并化简．）
（2）假如这个单位现组织包括管理员工在内的共20名员工到北京旅游，该单位选择哪一家旅行社比较优惠？请说明理由．
（3）如果计划在五月份外出旅游七天，设最中间一天的日期为a，则这七天的日期之和为 ．（用含a的代数式表示，并化简．）
（4）假如这七天的日期之和为63的倍数，则他们可能于五月几号出发？（写出所有符合条件的可能性，并写出简单的计算过程．）
小亮家购买了一套保障房，准备将地面铺上地砖，地面结构如图所示，根据图中的数据（单位：
），解答下列问题：
（1）写出用含x、y的代数式表示地面的总面积（结果要化简）；
（2）若卫生间和厨房的面积之和是卧室面积的
，且地面总面积是卫生间面积的15倍，铺12地砖的平均费用为80元，求铺地砖的总费用为多少元？
甲、乙两家文具商店出售同样的钢笔和本子．钢笔每支18元，本子每本2元．甲商店推出的优惠方法为买一支钢笔送两本本子；乙商店的优惠方法为按总价的九折优惠．小丽想购买5支钢笔，本子
本（≥10）
（1）若到甲商店购买，应付 元（用代数式表示）．
（2）若到乙商店购买，应付 元（用代数式表示）．
（3）若小丽要买本子10本，应选择那家商店？若买100本呢？
我国出租车收费标准因地而异．甲市为：起步价（行驶路程不超过3千米）6元，3千米后每千米（不足1千米，按1千米计算）价格1．5元；乙市为：起步价10元，3千米后每千米价格1．2元．
（1）试问在甲、乙两市乘坐出租车s（s＞3）千米的价钱差是多少元？
（2）如果在甲、乙两市乘坐出租车的路程都是10千米，那么哪个市的收费标准高？高多少？
定义一种新运算，满足下列等式，请你细心观察下列各式：
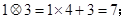
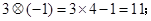
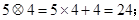
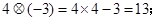
（1）仿照上面式子你可得出：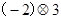
=____________________；
（2）经过探究你可猜想：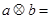 
_____________________；
（3）如果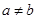
，上面你所得到的算式满足交换律吗？为什么？
（4）如果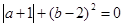
，试求
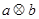的值．
某城市为了鼓励居民节约用水，对自来水用户按如下标准收费：若每月每户用水的最高标准为10吨，超过标准的部分加价收费，不超过10吨，每吨按2.9元收费，超过10吨的部分按每吨4元收费，
（1）某用户3月份用水x吨，请用含x的代数式表示应交水费
（2）求当x=25时的水费．
（1）当
时，求代数式
的值．
（2） 已知
的值为7 , 求代数式
的值
已知|x-2|+（y+1）2=0．
（1）求x、y的值；
（2）求-x3+y4的值．
时，求代数式
的值．
的值为7 , 求代数式
的值
cm，第二边比第一边长
，第三边比第二边短2acm，
，
时，求三角形的周长的值是多少？
（1）求
的值。（2）求
的值。
粤公网安备 44130202000953号