如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: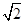 ≈1.414,
≈1.414,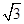 ≈1.732)
≈1.732)
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( ).
A. |
B. |
C. |
D.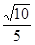 |
2015年4月25日14时11分尼泊尔发生了8.1级大地震.山坡上有一棵与水平面垂直的大树,大地震过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4米.
(1)求∠DAC的度数;
(2)求这棵大树原来的高度是多少米?(结果精确到个位,参考数据: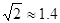 ,
, ,
,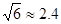 )
)
在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
(1)求tan∠FOB的值;
(2)用含t的代数式表示△OAB的面积S;
如图,小红站在水平面上的点A处,测得旗杆BC顶点C的仰角为60°,点A到旗杆的水平距离为a米.若小红的水平视线与地面的距离为b米,则旗杆BC的长为________米。(用含有a、b的式子表示)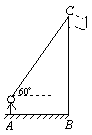
如图,甲楼AB的高度为35m,经测得,甲楼的底端B处与乙楼的底端D处相距105m,从甲楼顶部A处看乙楼顶部C处的仰角∠CAE的度数为25°.求乙楼CD的高度(结果精确到0.1m).[参考数据:sin25°=0.42,cos25°=0.91,tan25°=0.47].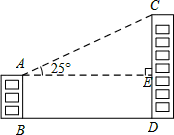
如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为
| A.20米 | B.10 米 米 |
C.15 米 米 |
D.5 米 米 |
如图,港口A在观测站O的正东方向,OA="4" km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为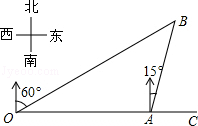
| A.4km | B. km km |
C.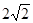 km km |
D.( km km |
如图,“和谐号”高铁列车的小桌板收起时,小桌板的支架底端与桌面顶端的距离OA=75厘米,且可以近似看作与地面垂直.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
阅读下面材料:
小红遇到这样一个问题:如图1,在四边形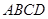 中,
中,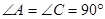 ,
,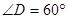 ,
,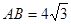 ,
, ,求
,求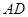 的长.
的长.
小红发现,延长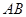 与
与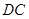 相交于点
相交于点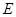 ,通过构造Rt△
,通过构造Rt△ ,经过推理和计算能够使问题得到解决(如图2).
,经过推理和计算能够使问题得到解决(如图2).
(1)请回答: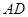 的长为 .
的长为 .
(2)参考小红思考问题的方法,解决问题:
如图3,在四边形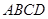 中,
中, ,
,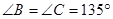 ,
,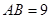 ,
, ,求
,求 和
和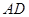 的长.
的长.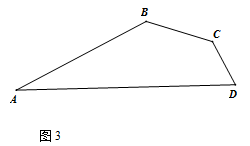
(本题10分)如图,一楼房AB后有一假山,其斜坡CD坡比为1: ,山坡坡面上点 E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
,山坡坡面上点 E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
(1)求点E距水平面BC的高度;
(2)求楼房AB的高。(结果精确到0.1米,参考数据 ≈1.414,
≈1.414, ≈1.732).
≈1.732).
如图所示,体育场内一看台与地面所成夹角为
,看台最低点A到最高点B的距离为
,
,
两点正前方有垂直于地面的旗杆
.在
,
两点处用仪器测量旗杆顶端
的仰角分别为
和
(仰角即视线与水平线的夹角)
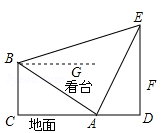
(1)求
的长;
(2)已知旗杆上有一面旗在离地1米的F点处,这面旗以0.5米/秒的速度匀速上升,求这面旗到达旗杆顶端需要多少秒?