如图,一只蚂蚁从 点出发,沿着扇形
点出发,沿着扇形 的边缘匀速爬行一周,设蚂蚁的运动时间为
的边缘匀速爬行一周,设蚂蚁的运动时间为 ,蚂蚁到
,蚂蚁到 点的距离为
点的距离为 ,则
,则 关于
关于 的函数图象大致为
的函数图象大致为
从重庆到成都的动车从重庆站出发,匀加速行驶一段时间后开始匀速行驶,过了一段时间,火车到达下一个车站停下,上下完旅客后,火车又匀加速行驶,一段时间后再次开始匀速行驶,那么可以近似地刻画出火车在这段时间内的速度变化情况的图像是( )
如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数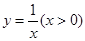 的图象上,则点E的坐标是( )
的图象上,则点E的坐标是( )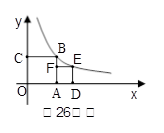
A.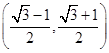 |
B.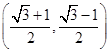 |
C.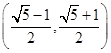 |
D.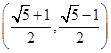 |
小明的爸爸早晨出去散步,从家走了20分到达距离家800米的公园,他在公园休息了10分,然后用30分原路返回家中,那么小明的爸爸离家的距离S(单位:米)与离家的时间t(单位:分)之间的函数关系图象大致是( )
某企业信息部进行市场调研发现:
信息一:如果单独投资A种产品,所获利润yA(万元)与投资金额x(万元)之间存在某种关系的部分对应值如下表:
| x(万元) |
1 |
2 |
2.5 |
3 |
5 |
| yA(万元) |
0.4 |
0.8 |
1 |
1.2 |
2 |
信息二:如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间存在二次函数关系:yB=ax2+bx,且投资2万元时获利润2.4万元,当投资4万元时,可获 利润3.2万元.
利润3.2万元.
(1)求出yB与x的函数关系式.
(2)从所学过的一次函数、二次函数、反比例函数中确定哪种函数能表示yA与x之间的关系,并求出yA与x的函数关系式.
(3)如果企业同时对A、B两种产品共投资15万元,请设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?
每个小方格都是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系中的位置如图所示。

(1)将菱形OABC先向右平移4个单位,再向上平移2个单位,得到菱形O1A1B1C1,请画出菱形O1A1B1C1;
(2)将菱形OABC绕原点O顺时针旋转90º,得到菱形OA2B2C2,请画出菱形OA2B2C2,并写出点A2、B2、C2三点的坐标
如图,在平面直角坐标系中,四边形ABCD的四个顶点的坐标分别是A(1,3)、
B(2,2)、C(2,1),D(3,3).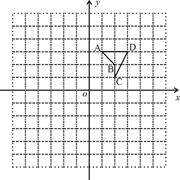
(1)以原点O为位似中心,相似比为2,将图形放大,画出符合要求的位似四边形;
(2)在(1)的前提下,写出点A的对应点坐标A′
如图,所示的计算程序中,y与x之间的函数关系对应的图象所在的象限是

| A.第一象限 | B.第一、三象限 | C.第二、四象限 | D.第一、四象限 |
已知点P(a-1,a+2)在平面直角坐标系的第二象限内,则a的取值范围在数轴上可表示为(阴影部分)

如图是胡老师画的一幅写生画,四位同学对这幅画的作画时间作了猜测. 根据胡老师给出的方向坐标,猜测比较合理的是 ( )
| A.小明:“早上8点” | B.小亮:“中午12点” |
| C.小刚:“下午5点” | D.小红:“什么时间都行” |