初中数学计算器—基础知识试题

如图13，在等腰中，，，点从点开始沿边以每秒1 的速度向点运动，点从点开始沿边以每秒2 的速度向点运动，保持垂直平分，且交于点，交于点．点分别从两点同时出发，当点运动到点时，点、停止运动，设它们运动的时间为．
（1）当=      秒时，射线经过点；

（2）当点运动时，设四边形的面积为，求与的函数关系式(不用写出自变量取值范围)；
（3）当点运动时，是否存在以为顶点的三角形与△相似？若存在，求出的值；若不存在，请说明理由．

如图11，正比例函数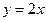的图像与一次函数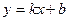的图像交于点A(ｍ，2)， 一次函数图像经过点B 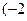, 与y轴的交点为C与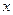轴的交点为D．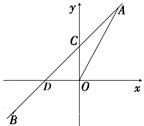

（1）求一次函数解析式；
（2）求C点的坐标；
（3）求△AOD的面积。

如图4，市政府准备修建一座高AB＝6m的过街天桥，已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为，则坡面AC的长度为

A．m

B．10 m

C．m

D．m

某校八年级同学到距学校6km的郊外春游，一部分同学步行，另一部分同学骑自行车，沿相同路线前往，如图分别表示步行和骑车的同学前往目的地所走的路程与所用时间x(min)之间的函数图象，则以下判断错误的是（   ）

A．骑车的同学比步行的同学晚出发30min

B．步行的速度是6km/h

C．骑车的同学从出发到追上步行的同学用了20min

D．骑车的同学和步行的同学同时到达目的地

点P的坐标是(4，一8)，则P点关于原点的对称点P1的坐标是(   )[

A．(—4，一8)

B．(4,8)

C．(4，一8)

D．(-4，8)

“水立方”的游泳池长为50m，宽为25m，深为3m.现以x m/min的速度向池中注
水，注满水池需y min，则y与x函数关系的大致图象为（     ）
 

若点M（a，b）在第二象限，则点（，b）是在（   ）

A．第一象限

B．第二象限

C．第三象限

D．第四象限

P点在第二象限，到y轴的距离是4，到x轴的距离是3，则P点的坐标是           .

在函数y＝中，自变量x的取值范围是             （ ▲ ）

A．x＞2

B．x≥2

C．x≠0

D．x≠2

如图，已知点F的坐标为（3，0），点A、B分别是某函数图像与x轴、y轴的交点，点P 是此图像上的一动点，设点P的横坐标为x，PF的长为d，且d与x之间满足关系：d=5－x(0≤x≤5)，则结论：① AF= 2 ② BF=4  ③ OA=5  ④ OB=3，正确结论的序号是 
                   
A．①②③    B ①③  C．①②④   D．③④

函数y=中，自变量x的取值范围是

A．

B．

C．

D．

函数自变量的取值范围为：                      ；

如图是某蓄水池的横断面示意图，分为深水池和浅水池，如果这个蓄水池以固定的流量注水，下面图象中，能大致表示水的最大深度h与时间t之间的关系是（　 　）

在比例尺为1:5000的地图上,量得甲,乙两地的距离为25cm,则甲,乙两地的实际距离是(     )

A．1.25km

B．12.5km

C．125km

D．1250km

函数中，自变量的取值范围是            .