初中数学计算器—基础知识解答题

如图，在平面直角坐标系中，已知点A（0，2），点P是x轴上一动点，以线段AP为一边，在其一侧作等边三角线APQ．当点P运动到原点O处时，记Q的位置为B．
（1）求点B的坐标；
（2）求证：当点P在x轴上运动（P不与O重合）时，∠ABQ为定值；

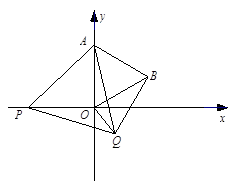
（3）是否存在点P，使得以A、O、Q、B为顶点的四边形是梯形？若存在，请求出P点的坐标；若不存在，请说明理由．

（1）在图1中，平行四边形ABCD的顶点A，B，C，D的坐标（如图），请写出图中的顶点C的坐标（　_________　，　_________　）．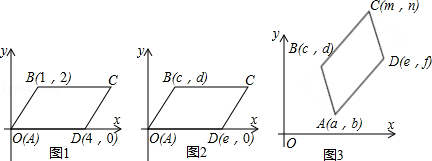

（2）在图2中，平行四边形ABCD的顶点A，B，C，D的坐标（如图），求出图中的标点C的坐标，并说明理由（C点坐标用含c，d，e的代数式表示）．
归纳与发现
（3）通过对图1，2的观察，你会发现：图3中的平行四边形ABCD的顶点坐标为A（a，b），B（c，d），C（m，n），D（e，f）时，则横坐标a，c，m，e之间的等量关系为　_________　．

已知动点P以每秒2cm的速度沿如图所示的边框按从B⇒C⇒D⇒E⇒F⇒A的路径移动，相应的△ABP的面积S关于时间t的函数图象如图所示，若AB=6cm，试回答下列问题：
（1）动点P在线段                上运动的过程中△ABP的面积S保持不变．
（2）BC=      cm;  CD=      cm;   DE=      cm;   EF=      cm
（3）求出图乙中的a与b的值．

如图，函数的图象与函数（x＞0）的图象交于A（a，1）、B（1，b）两点．

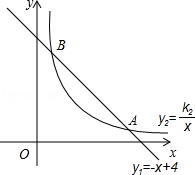
（1）求函数y₂的表达式；
（2）观察图象，比较当x＞0时，y₁与y₂的大小．

（本小题满分9分）我市准备在相距2千米的M，N两工厂间修一条笔直的公路，但在M地北偏东45°方向、N地北偏西60°方向的P处，有一个半径为0.6千米的住宅小区（如图），问修筑公路时，这个小区是否有居民需要搬迁？（参考数据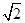：≈1.41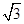，≈1.73）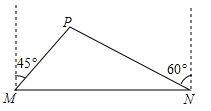

(1)计算：
（2）化简：

如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（﹣1，2），B（﹣3，4）C（﹣2，6）

（1）画出△ABC绕点A顺时针旋转90°后得到的△A₁B₁C₁
（2）以原点O为位似中心，画出将△A₁B₁C₁三条边放大为原来的2倍后的△A₂B₂C₂．

在平面直角坐标系xOy中，已知A（－1，5），B（4，2），C（－1，0）三点。
（1）点A关于原点O的对称点A′的坐标为     ，点B关于x轴对称点B′的坐标为     ，点C关于y轴对称点C′的坐标为     ；
（2）求（1）中的△A′B′C′的面积。

小虎一家利用元旦三天驾车到某景点旅游，小汽车出发前油箱有油36L，匀速行驶若干小时后，油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示，根据图象回答下列问题：

（1）求油箱余油量Q与行驶时间t之间的函数关系式；
（2）如果出发地距景点200km，车速为80km/h，要到达景点，油箱中的油是否够用？请说明理由．

如图1，已知直线与y轴交于点A，抛物线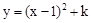经过点A，其顶点为B，另一抛物线的顶点为D，两抛物线相交于点C

（1）求点B的坐标，并说明点D在直线的理由；
（2）设交点C的横坐标为m
①交点C的纵坐标可以表示为：        或        ，由此请进一步探究m关于h的函数关系式；
②如图2，若，求m的值

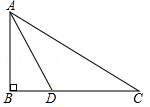
数学活动课上，老师和学生一起去测量学校升旗台上旗杆AB的高度，如图，老师测得升旗台前斜坡FC的坡比为i_FC=1：10（即EF：CE=1：10），学生小明站在离升旗台水平距离为35m（即CE=35m）处的C点，测得旗杆顶端B的仰角为α，已知tanα=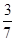，升旗台高AF=1m，小明身高CD=1.6m，请帮小明计算出旗杆AB的高度．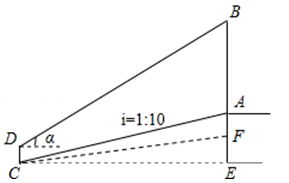

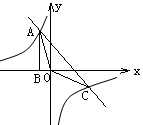
如图，Rt△ABO的顶点A是双曲线y=与直线y=-x-（k+1）在第二象限的交点.AB⊥x轴于B，且.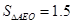

（1）求这两个函数的解析式；
（2）求直线与双曲线的两个交点A、C的坐标和△AOC的面积.并根据图像写出；
（3）方程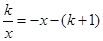的解；
（4）使一次函数的值大于反比例函数的值的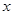的取值范围；

已知一次函数的图像经过点（—2，－2）和点（2，4）
（1）求这个函数的解析式；
（2）求这个函数的图像与y轴的交点坐标。

如图，某中学九年级数学兴趣小组测量校内旗杆AB的高度，在C点测得旗杆顶端A的仰角∠BCA=30°，向前走了20米到达D点，在D点测得旗杆顶端A的仰角∠BDA=60°，求旗杆AB的高度．（结果保留根号）

（1）计算：；
（2）解不等式，并将其解集表示在数轴上．