2015年初中毕业升学考试(四川内江卷)数学
有一组数据如下:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是( )
| A.10 | B.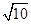 |
C.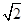 |
D.2 |
某十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是黄灯的概率为( )
A.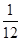 |
B.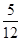 |
C. |
D.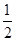 |
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )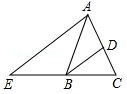
| A.40° | B.45° | C.60° | D.70° |
植树节这天有20名同学共种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵.设男生有x人,女生有y人,根据题意,下列方程组正确的是( )
A.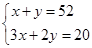 |
B.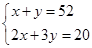 |
C. |
D.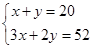 |
如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为( )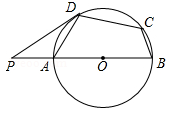
| A.40° | B.35° | C.30° | D.45° |
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )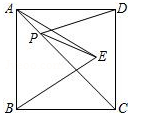
A.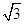 |
B.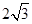 |
C. |
D. |
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线 与正方形ABCD有公共点,则k的取值范围为( )
与正方形ABCD有公共点,则k的取值范围为( )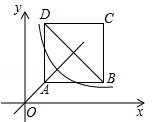
| A.1<k<9 | B.2≤k≤34 | C.1≤k≤16 | D.4≤k<16 |
如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为 .
(本小题满分9分)如图,将▱ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.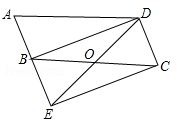
(1)求证:△ABD≌△BEC;
(2)连接BD,若∠BOD=2∠A,求证:四边形BECD是矩形.
(本小题满分9分)为了掌握我市中考模拟数学试题的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为160分)分为5组:第一组85~10;第二组100~115;第三组115~130;第四组130~145;第五组145~160,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列问题: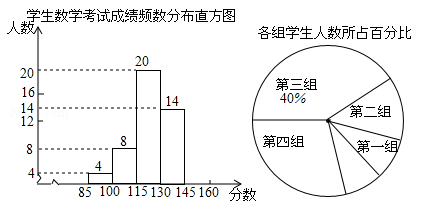
(1)本次调查共随机抽取了该年级多少名学生?并将频数分布直方图补充完整;
(2)若将得分转化为等级,规定:得分低于100分评为“D”,100~130分评为“C”,130~145分评为“B”,145~160分评为“A”,那么该年级1500名考生中,考试成绩评为“B”的学生大约有多少名?
(3)如果第一组只有一名是女生,第五组只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想,请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
(本小题满分9分)我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据: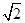 ≈1.41,
≈1.41,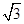 ≈1.73)
≈1.73)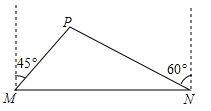
(本小题满分10分)某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润;
(3)实际进货时,厂家对电冰箱出厂价下调k(0<k<100)元,若商店保持这两种家电的售价不变,请你根据以上信息及(2)问中条件,设计出使这100台家电销售总利润最大的进货方案.
在平面直角坐标系xOy中,过点P(0,2)作直线l: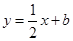 (b为常数且b<2)的垂线,垂足为点Q,则tan∠OPQ= .
(b为常数且b<2)的垂线,垂足为点Q,则tan∠OPQ= .
如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE;②HO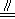
 BG;③S正方形ABCD:S正方形ECGF=1:
BG;③S正方形ABCD:S正方形ECGF=1: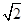 ;④EM:MG=1:(
;④EM:MG=1:(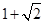 ),其中正确结论的序号为 .
),其中正确结论的序号为 .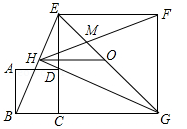
如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.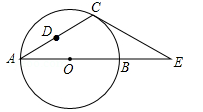
(1)试说明CE是⊙O的切线;
(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;
(3)设点D是线段AC上任意一点(不含端点),连接OD,当 CD+OD的最小值为6时,求⊙O的直径AB的长.
CD+OD的最小值为6时,求⊙O的直径AB的长.
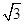



 中自变量x的取值范围是( )
中自变量x的取值范围是( )

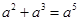
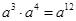

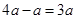
 = .
= . +
+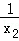 =3,则k的值是 .
=3,则k的值是 .
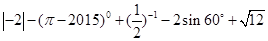 .
. ,
,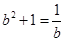 ,则
,则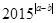 |= .
|= .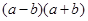 = ;
= ; = ;
= ;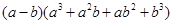 = .
= .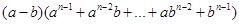 = (其中n为正整数,且
= (其中n为正整数,且 ).
).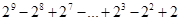 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号