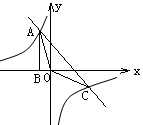
如图,Rt△ABO的顶点A是双曲线y= 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且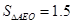 .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.并根据图像写出;
(3)方程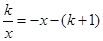 的解;
的解;
(4)使一次函数的值大于反比例函数的值的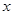 的取值范围;
的取值范围;
让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系。
第一步:数轴上两点连线的中点表示的数
自己画一个数轴,如果点A、B分别表示-2、4,则线段AB的中点M表示的数是 。 再试几个,我们发现:
数轴上连结两点的线段的中点所表示的数是这两点所表示数的平均数。
第二步;平面直角坐标系中两点连线的中点的坐标(如图①)
为便于探索,我们在第一象限内取两点A(x1,y1),B(x2,y2),取线段AB的中点M,分别作A、B到x轴的垂线段AE、BF,取EF的中点N,则MN是梯形AEFB的中位线,故MN⊥x轴,利用第一步的结论及梯形中位线的性质,我们可以得到点M的坐标是( , )(用x1,y1,x2,y2表示),AEFB是矩形时也可以。我们的结论是:平面直角坐标系中连结两点的线段的中点的横(纵)坐标等于这两点的横(纵)坐标的平均数。

图① 图②
第三步:平面直角坐标系中平行四边形的顶点坐标之间的关系(如图②)
在平面直角坐标系中画一个平行四边形ABCD,设A(x1,y1),B(x2,y2),C(x3,y3),
D(x4,y4),则其对角线交点Q的坐标可以表示为Q( , ),也可以表示为Q( , ),经过比较,我们可以分别得出关于x1,x2,x3,x4及,y1,y2,y3,y4的两个等式是 和 。 我们的结论是:平面直角坐标系中平行四边形的对角顶点的横(纵)坐标的 。
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)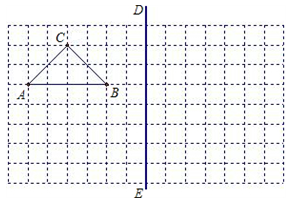
(1)画出格点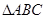 (顶点均在格点上)关于直线
(顶点均在格点上)关于直线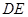 对称的
对称的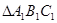 ;
;
(2)在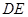 上画出点
上画出点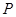 ,使
,使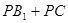 最小;
最小;
(3)在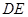 上画出点
上画出点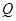 ,使
,使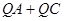 最小.
最小.
如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西37°方向上,AP=30海里.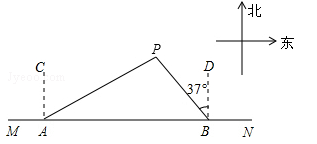
(1)尺规作图:过点P作AB所在直线的垂线,垂足为E(要求:保留作图痕迹,不写作法);
(2)求船P到海岸线MN的距离(即PE的长);
(3)若船A、船B分别以20海里/时、15海里/时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果保留根号)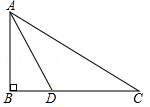
(本小题满分8分)如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据: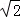 ≈1.414,
≈1.414, ≈1.732)
≈1.732)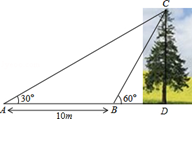
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上一动点,连结CD,DE,以CD,DE为边作□CDEF。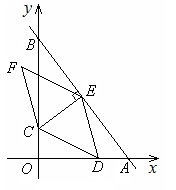
(1)当0< m <8时,求CE的长(用含m的代数式表示);
(2)当m =3时,是否存在点D,使□CDEF的顶点F恰好落在y轴上?若存在,求出点D的坐标;若不存在,请说明理由;
(3)点D在整个运动过程中,若存在唯一的位置,使得□CDEF为矩形,请求出所有满足条件的m的值。
(本题6分)为了乘车方便,张强同学买了100元的乘车月票卡,如果他乘车的次数用x表示,则记录他每次乘车后的余额y(元)如下表:
(1)写出用乘车的次数x表示余额y的式子;
(2)利用上述式子,帮张强算一算乘了15次车还剩多少元?
(3)张强用100元的乘车月票卡最多乘几次车?
如图1,已知直线 与y轴交于点A,抛物线
与y轴交于点A,抛物线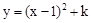 经过点A,其顶点为B,另一抛物线
经过点A,其顶点为B,另一抛物线 的顶点为D,两抛物线相交于点C
的顶点为D,两抛物线相交于点C
(1)求点B的坐标,并说明点D在直线 的理由;
的理由;
(2)设交点C的横坐标为m
①交点C的纵坐标可以表示为: 或 ,由此请进一步探究m关于h的函数关系式;
②如图2,若 ,求m的值
,求m的值
如图,已知一次函数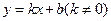 的图象与x轴、y轴分别交于A、B两点,且与反比例函数
的图象与x轴、y轴分别交于A、B两点,且与反比例函数 的图象在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,
的图象在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,
(1)求点A,B,D的坐标;
(2)求一次函数和反比例函数的解析式。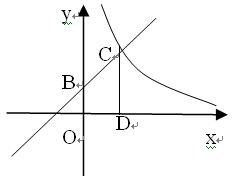
在平面直角坐标系中,点M的坐标为(a,1-2a).
(1)当a=-1时,点M在坐标系的第___________象限(直接填写答案);
(2)将点M向左平移2个单位,再向上平移1个单位后得到点N,当点N在第三象限时,求a的取值范围.
已知直线y = x+m与x轴、y轴分别交于点A、B,与双曲线y
= x+m与x轴、y轴分别交于点A、B,与双曲线y =
=  分别交于点C、D,且点C的坐标为(-1,2).
分别交于点C、D,且点C的坐标为(-1,2).分别求出直线AB及双曲线的函数表达式;
利用图像直接写出:当x在什么范围内取值时y
 >y
>y
如图,在东西方向的海岸线MN上有相距10海里的A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,船P在船B的北偏西45°方向上.求船P到海岸线MN的距离(结果保留根号).